Перевод римских чисел в десятичные. конвертер систем счисления

Обозначение и правила записи, узловые числа

Считается, что возникновение римских цифр связано с жестами:

• I — палец;
• V — ладонь;
• Х — перекрещенные ладони.

100 и 1000 обозначаются буквами C и М, предположительно по первым буквам латинских числительных.
Для записи используют семь букв, обозначающие узловые числа:

• I — 1;
• V — 5;
• X — 10;
• L — 50;
• C — 100;
• D — 500;
• M — 1000.

Разряды идут слева направо: тысячи, сотни, десятки, единицы. Ноль отсутствует, хотя в античности иногда записывали его буквой N. 

Для упрощения записи есть два правила:

1. Когда большая цифра находится перед меньшей, их нужно сложить.
2. Когда меньшая цифра находится перед большей, меньшую нужно вычесть из нее.

Пример

Расшифруем запись римскими цифрами — число ХLIX: (50–10) + (10–1) = 40 + 9 = 49.

Методы для группировки данных по полю,полям в Таблице Значений на примере универсального метода списания по партиям, а также отбора строк в ТЗ по произвольному условию. Для 8.x и 7.7 Промо

Я очень часто использую группировку данных по полю и полям, как в восьмерке, так и в семерке. Это аналог запроса Итоги, но там строится дерево, а в большинстве случаев нужны «плоские данные». Да и делать запрос в большинстве случаев более накладный процесс, чем работа с ТЗ.
Все достоинства такого подхода приведены на примере метода универсального списания по париям, а так же отбора строк в ТЗ по произвольному условию.
Для 7.7 еще отчеты сравнения двух ТЗ. Работая с различными базами для упрощения сравнения номенклатуры, или как аналог джойнов(join), сделал сравнение двух таблиц значений по нескольким полям. Пока группировки полей должны быть уникальны.
Часто приходится искать дубли, для универсального поиска есть ДублиВТзПоПолю и пример в Тест.ert.

1 стартмани

[Разработчику] Любая таблица значений в OLAP Промо

Анализируем различные данные в 1С, используя OLAP-технологии со всеми прелестями. Т.е. наглядное отображение данных, быстрые расчеты, горизонтальные и вертикальные группировки любой вложенности, удобная фильтрация, Drag’n’Drop и ещё много приятных вещей от MS.

Обработка на входе принимает практически любую таблицу значений (ТЗ в которой колонкам указаны типы значений, строка, число и т.п.), на выходе имеем на форме 1С сводную таблицу и график по этой ТЗ, с которой работаем, как и в Excel со сводной таблицей и диаграммой.

Взял за основу разработку «OLAP Анализ счёта» ( http://infostart.ru/public/14964/ ) от JohnyDeath и переделал под любую ТЗ.

Опционально используется «Прогресс бар для 1С 77» (http://infostart.ru/public/14061/ ) от Gmix.

1 стартмани

Кратко об основных системах счисления

Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.

Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.

Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.

Шестнадцатеричная система счисления. Наиболее распространена в современных компьютерах. При помощи неё, например, указывают цвет. #FF0000 — красный цвет. Для записи числа используются цифры от 0 до 9 и буквы A,B,C,D,E,F, которые соответственно обозначают числа 10,11,12,13,14,15.

Примеры как в Excel перевести арабские цифры в римские

Пример 1. В таблице приведены арабские числа. Выполнить их преобразование к римским числам, если это возможно, и записать полученные значения в соседнем столбце.

Исходная таблица имеет следующий вид:

Для преобразований используем формулу:

Описание аргументов:

• РИМСКОЕ(A2:A11) – функция, возвращающая римские числа в результате преобразования данных, которые содержатся в диапазоне ячеек A2:A11;
• «Недопустимое число» – текстовая строка, возвращаемая функцией ЕСЛИОШИБКА, если преобразование данных функцией РИМСКОЕ невозможно.

Результат вычислений:

Благодаря процессу конвертирования функции нам удалось выполнить перевод всех арабских положительных чисел в римские цифры.

История появления римских цифр

Интересным является тот факт, что эти необычные цифры дошли до наших времен не из-за каких-либо оригинальных или полезных свойств. А именно из-за большого влияния римлян и Римской империи в прошлом. Даже когда в 7 веке до нашей эры этруски завоевали Рим, им пришлось почувствовать влияние средиземноморских культур на себе. Об этом можно судить исходя из того, что в их культуре сразу же произошли изменения, которые касаются в первую очередь представлением цифр в письме. После этих событий обе системы имели множество схожих элементов в числах.

В многих древних рукописях цифра пять (5) представлена в одном и том же виде — V. Но её достоверное происхождение не определено и по сей день. Одни историки утверждают, что знак символизирует раскрытую ладонь с прижатыми четырьмя пальцами и оттопыренным большим пальцем. Множество споров вызвала римская цифра десять (10) — X. Её происхождение также связывают с человеческими конечностями — руками. Римская «десятка» символизирует скрещенные руки. Таким образом, во многих отраслях производства (например, в строительстве) римляне могли показать друг другу числовые значения, используя руки.

До сих пор не установлен источник возникновения римских цифровых знаков. Но были замечены заимствования элементов символов из других народов. Например, римские цифры сто и тысяча похожи на некоторые древнегреческие буквы. Известно также, что римляне не были склонны и заинтересованы в глубоких познаниях математики. Поэтому их представление максимального числа сегодня выглядит смешным — 399 999. Дробных представлений чисел римляне вовсе избегали. Иногда, если это было слишком необходимо, определенную единицу измерения делили на 12. Сегодня такой прием также используется, когда мы выражаем длину в футах, дюймах и пр.

Правила выполнения арифметических операций с числами

1. Сложение и вычитание.

   Сложить два римских числа достаточно просто. Например:

   $XIX + XXVI = XXXV$

   Сложение выполняется в следующей последовательности:

   а) $IX + VI = XV$ ($I$ после $V$ «уничтожает» $I$ перед $X$);

   б) $X + XX = XXX$ (при добавлении еще одного $X$, получаем $XXXX$, или $XL$).

   Сложность вычитания римских чисел приблизительно такая же. Например, для вычитания из $500$ числа $263$ уменьшаемое число необходимо для начала разложить на более мелкие составляющие, а затем сократить повторяющиеся в уменьшаемом и вычитаемом знаки:

   $D — CCLXIII = CCCCLXXXXVIIIII — CCLXIII = CCXXXVII$

2. Умножение.

   С умножением дело обстояло гораздо сложнее.

   Допустим, требовалось умножить $126$ на $37$ (у римлян знаков действий не было, названия действий писали словами).

   $CXXVI \cdot XXXVII$

   Приходилось умножать множимое на каждую цифру множителя отдельно, а затем складывать все произведения.

   Такая техника выполнения умножения аналогична умножению многочленов.

3. Деление.

   Выполнение деления было очень сложным в римской системе счисления. Для этого использовался специальный инструмент – абак (древние счеты). Только высоко образованные люди умели и могли работать с ним.

Расчёт параметров стропильной системы

Римские цифры

От 1 до 50

Таблица 1 . Самые распространенные римские цифры

Арабские	Римские
1	I
2	II
3	III
4	IV
5	V
6	VI
7	VII
8	VIII
9	IX
10	X
11	XI
12	XII
13	XIII
14	XIV
15	XV
16	XVI
17	XVII
18	XVIII
19	XIX
20	XX
21	XXI
22	XXII
23	XXIII
24	XXIV
25	XXV
26	XXVI
27	XXVII
28	XXVIII
29	XXIX
30	XXX
31	XXXI
32	XXXII
33	XXXIII
34	XXXIV
35	XXXV
36	XXXVI
37	XXXVII
38	XXXVIII
39	XXXIX
40	XL
41	XLI
42	XLII
43	XLIII
44	XLIV
45	XLV
46	XLVI
47	XLVII
48	XLVIII
49	XLIX
50	L

От 10 до 100, от 100 до 3000

Таблица 2 . Приведены числа кратные 10 (от 10 до 100).

Арабские	Римские
10	X
20	XX
30	XXX
40	XL
50	L
60	LX
70	LXX
80	LXXX
90	XC
100	C

Таблица 3 . Приведены числа, кратные 50 (от 50 до 1000).

Арабские	Римские
50	L
100	C
150	CL
200	CC
250	CCL
300	CCC
350	CCCL
400	CD
450	CDL
500	D
550	DL
600	DC
650	DCL
700	DCC
750	DCCL
800	DCCC
850	DCCCL
900	CM
950	CML
1000	M

Таблица 4 . Приведены числа, кратные 100 (от 100 до 3000).

Арабские	Римские
100	C
200	CC
300	CCC
400	CD
500	D
600	DC
700	DCC
800	DCCC
900	CM
1000	M
1100	MC
1200	MCC
1300	MCCC
1400	MCD
1500	MD
1600	MDC
1700	MDCC
1800	MDCCC
1900	MCM
2000	MM
2100	MMC
2200	MMCC
2300	MMCCC
2400	MMCD
2500	MMD
2600	MMDC
2700	MMDCC
2800	MMDCCC
2900	MMCM
3000	MMM

Перевод арабского числа в римское (и наоборот)

Разумеется вручную переводить (считая тысячи, сотни, и десятки) арабские числа в римские — занятие то еще (и вряд ли кто-то этим занимается, кроме может быть каких-нибудь математиков или историков).

Поэтому для этих целей гораздо удобнее пользоваться программами, которые могут за вас все посчитать и конвертировать. Благо, что для расчетов ничего сложнее, чем Excel или Word ненужно (да и их если нет — можно воспользоваться аналогами, в том числе и онлайн-версиями).

Способ 1 (Excel)

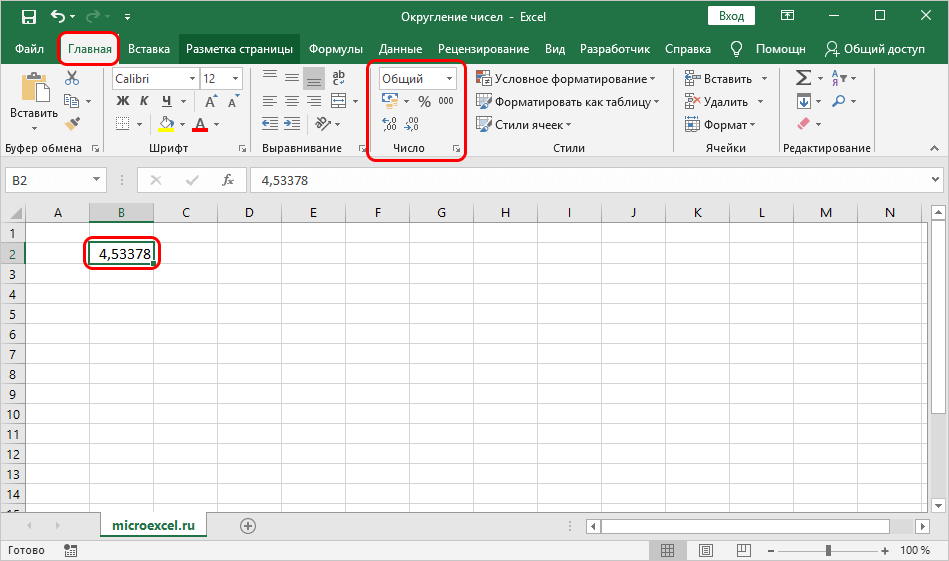
Один из самых простых способов перевести обычное число в римское — это воспользоваться спец. функцией Excel (тем более, что Microsoft Office есть практически на каждом втором ПК) . Кстати, если вы никогда не работали с Excel — то заранее предупреждаю, что написание обычных формул ничуть не сложнее, чем набрать какое-нибудь слово в тексте.

1) Если у вас нет Excel — можно установить его бесплатный аналог (например, Libre Office) — https://ocomp.info/chem-zamenit-word-i-excel.html#LibreOffice

2) Кроме этого, можно воспользоваться Яндекс-диском: в его арсенале так же есть онлайн-версия Excel.

Яндекс-диск — создать таблицу

И так, будем считать, что Excel (или его аналог) у вас есть, и программа запущена — перед вами большой лист в клеточку. Теперь выберите первую ячейку A1, и в верхнюю строку с формулой напишите:

где 355 — число, которое вам нужно конвертировать в римское.

После нажмите Enter. Программа автоматически покажет вам в ячейке A1 римское число (см. пример на скрине ниже). Теперь можно скопировать его и вставить в любой другой документ/текст.

Libre Office (или Excel) — формула перевода в римское число

Если вам в последствии понадобиться другое число — просто поменяйте его в формуле (в скобках) и Excel тут же покажет вам новый результат.

Для обратного перевода используется другая формула:

где LXXX — римское число

Обратите внимание на кавычки — они обязательны, т.к. римские числа задаются текстом

Формула перевода римского числа в арабское

Способ 2 (Word)

Если первый способ вам показался сложным (или вылезла какая-нибудь ошибка) — то осуществить перевод можно и в Word (причем, в некоторых случаях это выполняется даже побыстрее) .

Я покажу свой пример на версии Office 2019 (в принципе, аналогично будет выполняться и в других современных версиях 2016, 2013).

Word — формат номеров страниц / Кликабельно

Далее укажите формат страниц в виде арабских чисел “1, 2, 3. ” и выберите нумерацию страниц с того числа, которое вам нужно перевести в римское. В моем примере 3569.

После чего просто выберите новый формат нумерации “I, II, III” и ву-а-ля — арабское число преобразуется в римское. Осталось только скопировать его и вставить в нужный вам текст.

Меняем формат и готово!

Способ 3 (Word)

В Word есть еще один способ, как можно быстро перевести число в римское:

1. сначала нажмите сочетание кнопок Ctrl+F9 — у вас появятся фигурные скобки;
2. в фигурных скобках напишите: =542\*Roman (где вместо 542 — можно поставить свое число);
3. нажмите F9 (пример на скриншоте ниже).

Источник статьи: http://ocomp.info/rimskie-tsifryi.html

Перевод чисел из одной системы счисления в другую

Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.

Перевод чисел из любой системы счисления в десятичную систему счисления

Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:

1. Перевести число в десятичную систему счисления.Решение: = = = Ответ: =

2. Перевести число в десятичную систему счисления.Решение: = = = Ответ: =

Перевод чисел из десятичной системы счисления в другую систему счисления

Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.

Перевод целой части числа из десятичной системы счисления в другую систему счисления

Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.

3. Перевести число в восьмиричную систему счисления.Решение: 273 / 8 = 34 и остаток 1, 34 / 8 = 4 и остаток 2, 4 меньше 8, поэтому вычисления завершены. Запись из остатков будет иметь следующий вид: 421Проверка: = = = , результат совпал. Значит перевод выполнен правильно.Ответ: =

Рассмотрим перевод правильных десятичных дробей в различные системы счисления.

Перевод дробной части числа из десятичной системы счисления в другую систему счисления

Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.

4. Перевести число в двоичную систему счисления.Решение: (0 — целая часть, которая станет первой цифрой результата), (0 — вторая цифра результата), (1 — третья цифра результата, а так как дробная часть равна нулю, то перевод завершён).Ответ: =

Латинские (римские) цифры

Для обозначения цифр в латинском языке приняты комбинации следующих семи знаков: 1(1), V(5), X(10), L(50), С(100), D(500), M(1000). Если знак, обозначающий меньшее число, стоит справа от знака, обозначающего большее число, то меньшее число следует прибавлять к большему, если — слева, то вычитать, а именно:

• VI — 6, т. е. 5+1
• IV — 4, т. е. 5-1
• XI — 11, т. е. 10+1
• IX — 9, т. е. 10-1
• LX — 60, т. е. 50+10
• XL — 40, т. е. 50-10
• СХ — 110, т. е. 100+10
• ХС — 90, т. е. 100-10
• MDCCCXII — 1812, т. е. 1000+500+100+100+100+10+1+1
• MCMXVII — 1917, т. е. 1000+1000-100+10+5+1+1
• MCMLXI — 1961, т. е. 1000+1000-100+50+10+1

Ниже представлены латинские цифры, их текстовое написание и русское произношение:

• I (1) — unus .
• II (2) — duo .
• III (3) — tres .
• IV (4) — quattuor .
• V (5) — quinque .
• VI (6) — sex .
• VII (7) — septem .
• VIII (8) — octo .
• IX (9) — novem .
• X (10) — decem .
• XI (11) — undecim .
• II (12) — duodecim .
• XIII (13) — tredecim .
• XIV (14) — quattuordecim .
• XV (15) — quindecim .
• XVI (16) — sedecim .
• XVII (17) — septendecim .
• XVIII (18) — duodeviginti .
• XIX (19) — undeviginti .
• XX (20) — viqinti .
• XXI (21) — unus et viginti или viginti unus.
• XXII (22) — duo et viginti или viginti duo
• и т. д.
• XXVIII (28) — duodetriginta .
• XXIX (29) — undetriginta .
• XXX (30) — triginta .
• XL (40) — quadraginta .
• L (50) — quinquaginta .
• LX (60) — sexaginta .
• LXX (70) — septuaginta .
• LXXX (80) — octoginta .
• XC (90) — nonaginta .
• С (100) — centum .
• CC (200) — ducenti .
• CCC (300) — trecenti .
• CD (CCCC) (400) — quadringenti .
• D (500) — quingenti .
• DC (600) — sescenti или sexcenti .
• DCC (700) — septingenti .
• DCCC (800) — octingenti .
• CM (DCCCC) (900) — nongenti .
• M (1000) — mille .
• ММ (2000) — duo milia .
• V (5000) — quinque milia .
• X (10000) — decem milia .
• XX (20000) — viginti milia .
• С (100000) — centum milia .
• XI (1000000) — decies centena milia .

Римляне, как известно, использовали для записи числа латинские буквы. Считается, что римская система счисления является классическим примером непозиционной системы счисления, то есть такой системы счисления, в которой величина, которую обозначает цифра, не зависит от положения в числе. Напомним, что в римской системе счисления I обозначает 1, V обозначает 5, X — 10, L — 50, C — 100, D — 500, M — 1000. Например, число 3 в римской системе счисления будет обозначаться как III.

Однако на самом деле не все так просто, и она не является полностью непозиционной системой счисления, потому что в римской системе счисления есть дополнительное правило, которое влияет на величину, которую обозначает цифра, в зависимости от ее положения. Правило это запрещает употреблении одной и той же цифры более 3 раз подряд, поэтому три это III, а четыре это уже IV, и I(1), стоящая перед большей цифрой V(5), обозначает вычитание, то есть фактически равна -1.

Ниже два калькулятора — для перевода числа из диапазона 1 – 3999 в римское число и наоборот. Для чисел больше 3999 используется несколько другая нотация.

Как записывать римские цифры?

Записывать римские цифры нужно сначала с тысяч, затем идут сотни, потом десятки и только потом единицы.

Как, например, записать число 165 римскими цифрами? В числе 165 одна сотня, 6 десятков и 5 единиц. Смотрим по таблице: сотня записывается как С, 6 десятков — это пять десятков, которые обозначаются как L, плюс еще один десяток — это X. Пять единиц записываются как V. Соединяем это все вместе, получаем CLXV. Можете проверить число в конвертере в начале статьи.

Цифры, которые обозначают десятки — X, сотни — C, тысячи — M могут повторяться, чтобы записать большое число.

При их использовании, а также чисел пять — V, пятьдесять — L и пятьсот — D имеет значение позиция и других чисел, например, единица — I до пяти — V обозначает, что нужно V убавить, то есть IV — это 4.

А если меньшее число идет после, то значит нужно прибавлять: LX — здесь к 50 надо добавить 10, получим 60. Если добавить еще пару единичек, будет 62 — LXII.

XIX — это 19, а не 21, так как сначала считаем десятки, потом остальное. Десятков здесь один, дальше идет еще десятка без одного, то есть 9, на что указывает I перед X, вместе это дает — 19. Таким же образом вычисляются все остальные числа.

Все это может показаться кому-то очень сложным, поэтому вначале странички размещен конвертер римских цифр онлайн. Конвертировать цифры можно туда и обратно — обычные в римские, и римские — в обычные.

Также, нужно отметить, что в классической римской системе счисления цифры V, L, D повторяться не могут, а цифры I, X, С, M могут повторяться не более трех раз подряд, поэтому записать можно было число не более 3 999.

Хотя, конечно, впоследствии придумали обозначения и более крупных цифр, например, рисовали черту над символами, которая увеличивает их значение в тысячу раз, или же писали необходимое количество знаков, чтобы добиться необходимой величины. Есть и специальные символы, чтобы записывать подобные числа, однако, они уже не совпадают с буквами римского алфавита, а значит их невозможно будет ввести с клавиатуры. Поглядите на сводную таблицу таких больших чисел в римской записи:

4000	MV; ↀↁ; CIƆIƆƆ
5000	V; ↁ; IƆƆ
6000	VM; ↁↀ; IƆƆCIƆ
7000	VMM; ↁↀↀ; IƆƆCIƆCIƆ
8000	VMMM; ↁↀↀↀ; IƆƆCIƆCIƆCIƆ
9000	IX; ↀↂ; CIƆCCIƆƆ
10 000	X; ↂ; CCIƆƆ
20 000	XX; ↂↂ; CCIƆƆCCIƆƆ
30 000	XXX; ↂↂↂ; CCIƆƆCCIƆƆCCIƆƆ
40 000	XL; ↂↇ; CCIƆƆIƆƆƆ
50 000	L; ↇ; IƆƆƆ
60 000	LX; ↇↂ; IƆƆƆCCIƆƆ
70 000	LXX; ↇↂↂ; IƆƆƆCCIƆƆCCIƆƆ
80 000	LXXX; ↇↂↂↂ; IƆƆƆCCIƆƆCCIƆƆCCIƆƆ
90 000	XC; ↂↈ; CCIƆƆCCCIƆƆƆ
100 000	C; ↈ; CCCIƆƆƆ
200 000	CC; ↈↈ; CCCIƆƆƆCCCIƆƆƆ
300 000	CCC; ↈↈↈ; CCCIƆƆƆCCCIƆƆƆCCCIƆƆƆ
400 000	CD; CCCIƆƆƆIƆƆƆƆ
500 000	D; IƆƆƆƆ
600 000	DC; IƆƆƆƆCCCIƆƆƆ
700 000	DCC; IƆƆƆƆCCCIƆƆƆCCCIƆƆƆ
800 000	DCCC; IƆƆƆƆCCCIƆƆƆCCCIƆƆƆCCCIƆƆƆ
900 000	CM; CI; CCCIƆƆƆCCCCIƆƆƆƆ
1 000 000	M; I; CCCCIƆƆƆƆ

Пишем на клавиатуре

Практически все документы, дипломные работы, книги пишутся сейчас на компьютерах. В связи с этим возникает необходимость написания римских знаков на клавиатуре. На самом деле сделать это просто – можно пользоваться символами латинского алфавита. Стандартный вариант набора:

• переключаем клавиатуру на английский язык;
• нажимаем кнопку CapsLock , ведь римские значения пишутся верхним регистром латинской системы алфавита.

Если необходимо ввести длинную комбинацию, к примеру, 177, то для начала проводится вычисление: 100+70+7. После этого набираете с большего числа – CLXXVII. При написании очень больших цифр появляются сложности, в таком случае можно воспользоваться специальными числовыми конвертерами. Подобные онлайн сервисы можно поискать в сети, в свободном доступе есть и картинки с правильным обозначением.

Кроме того, для ввода цифр из Древнего Рима на компьютерных устройствах часто применяются специализированные ASCII коды, для их включения нужно — активировать режим Num Lock , затем, удерживая Alt , ввести определенное сочетание в дополнительной клавиатуре:

• Alt +73 – I;
• Alt +86 – V;
• Alt +88 – X;
• Alt +76 – L;
• Alt +67 – C;
• Alt +68 – D;
• Alt +77 – M.

Данный вариант на первый взгляд кажется сложным, но если работать с таблицей часто, можно быстро понять.

Автор рекомендует:

• Как поставить в Ворде ударение над буквой
• WPS Office — что это за программа, стоит ли её устанавливать?
• Как найти фотографию в интернете по фотографии
• Где найти и как запустить калькулятор на Windows 7/8/10: все способы
• Исправляем ошибку при направлении команды приложению Excel

Перевод из двоичной системы в шестнадцатеричную

Способ 1:

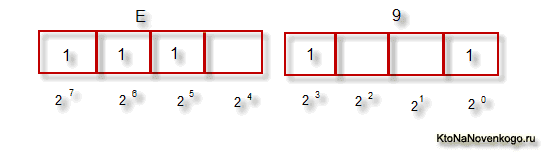
Разбиваем число на группы по 4 цифры справа налево. Последнюю (левую) группу дополним при необходимости ведущими нулями. Внутри каждой полученной группы произведем умножение каждой цифры на 2n, где n — номер разряда, и сложим результаты.

11010₂ = (0001) (1010) = (0*23 + 0*22 + 0*21 + 1*2) (1*23 + 0*22 + 1*21 + 0*2) = (0+0+0+1) (8+0+2+0) = (1) (10) = 1A₁₆

Способ 2:

Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:

Тетрада	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
Цифра	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

101111100₂ = (0001) (0111) (1100) = 17C₁₆

Римская система счисления: что из себя представляет и когда появилась

Определение

Система счисления — способ фиксации чисел в письменном виде с помощью определенных знаков. 

Римские цифры известны всему миру и широко применяются даже в XXI веке. Еще в XII веке европейцы считали римскими цифрами. Когда в 1202 году Леонардо Пизанский, также известный под прозвищем Фибоначчи, предложил копировать индо-арабскую десятичную систему в своей книге под названием «Liber Abaci», «Книга счетов», это спровоцировало горячие споры между ее поборниками «алгористами» и противниками «абакистами». Их противостояние растянулось в Европе на несколько веков, хотя в Италии перешли на римскую нумерацию уже в XIII веке.

Абакисты настаивали на том, что римские цифры и счетная доска превосходили письменные способы счисления алгористов. В конце концов, в XVI веке, когда римские цифры вышли из активного употребления на всей территории Европы, спор сошел на нет.

Это позиционная или непозиционная система

Системы делятся на три типа:

• позиционные;
• непозиционные;
• смешанные.

В позиционной системе разряд цифры четко связан с ее местом в записанном числе. Любое целое число в позиционной системе счисления — конечная линейная комбинация степеней ее основания.

Римская система отличается от позиционных систем использованием принципов сложения и вычитания. В непозиционных системах счисления место цифры в записи не имеет значения — например, во многих древних системах все записанные цифры нужно было складывать. Но если для каждого числа вводить уникальную цифру, это тяжело запомнить, поэтому люди придумывали способы обойтись ограниченным количеством цифр, называемых узловыми числами. В римской системе узловых чисел всего семь, самое крупное — тысяча, а записать с помощью этой системы можно числа до 3999. Поэтому для прочтения числа необходимо знать правила его записи. 

Почему используют римские цифры?

Так сложилось исторически. В античности и раннем средневековье римляне доминировали во всем, это была мировая империя, оказавшая огромное влияние на множество народов и самые разные области человеческой деятельности. Римский язык, а также их исчисление, использовались в литературе, философии, богословии, научных работах, причем еще много веков спустя после того, как Римская империя сошла с исторической сцены. Как отголосок этого — то, что люди до сих пор используют римские цифры в некоторых сферах своей жизни. Например, в русском языке римские цифры чаще всего используются при указании:

• века или тысячелетия: XX век, I тысячелетие до н.э.
• спряжения глагола
• группы крови
• монарха: Александр II, Людовик XIV
• тома какого-либо издания
• времени — на циферблатах часов под «старину»

А также в некоторых других случаях.

Правила выполнения арифметических операций с числами

Производить такие арифметические действия, как сложение и вычитание чисел, записанных римскими цифрами, можно в столбик, как и с арабскими, при необходимости расписывая их подробнее, т. е. раскладывая на более мелкие составляющие.

Пример

XIX + ХХVI = XVIIII + XXVI = XXXXV = XLV.

Пример

D — CC LX III = CCCC LXXXX VIIIII — CC LX III = CC XXX VII.

Чтобы перемножить числа, нужно умножать одно число на каждую цифру другого по отдельности.

Пример

\(XXI\times L=XXI\times XXXXX=(X+X+I)\times(X+X+X+X+X)=MXXXXX=ML.\\\)

Также существует интересный и, возможно, более удобный способ с использованием таблицы. Нужно начертить таблицу с клетками, разделенными по диагонали чертой, над таблицей написать первое число, а справа от нее — второе. В каждую клетку таблицы нужно вписать произведение цифр над клеткой и справа от нее, размещая над косой чертой десятки, а под ней — единицы. Затем нужно сложить числа в каждой косой полосе, выполняя это справа налево.

Так как делитель нельзя разбить на слагаемые, при делении римских чисел каждое предположение придется проверять умножением. Чтобы выяснить первую цифру частного, умножаем делитель на сто. Если произведение больше делимого, значит, в частном нет сотен. Тогда умножаем делитель на десять, двадцать и т. д. Когда произведение оказывается больше делимого, это значит, что предыдущее вычисление было верным. Выяснив количество десятков в частном, отнимаем от делимого делитель, умноженный на результат верного вычисления. Получив остаток, тем же способом вычисляем количество единиц.

Пример

Вычислим \(\frac{МСLХХVI}{XXVIII}.\\\)

Решение

\(XXVIII\times С=MMDCCC\\\)

\(XXVIII\times X=ССLХХХ\\\)

\(XXVIII \times XX = СССС L L ХХХХХХ = D L X\)

\(XXVIII \times XXX = DCCC\)

\(XXVIII \times XXXX = DD LL XX = MCXX\)

\(XXVIII \times L = MCXX + ССLХХХ = МСССL ХХХХХ = МСD\)

Произведение больше делимого, теперь производим вычисления с остатком:

\(MCLXXVI — MCXX = LVI\)

\(XXVIII \times I = XXVIII\)

\(XXVIII \times II = ХХХХVVIIIIII = LVI\)

Теперь, выяснив количество десятков и единиц в частном, получаем:

\(\frac{МСLХХVI}{XXVIII} = ХLII\)

Перевод из восьмеричной системы в двоичную

Способ 1:

Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.

Возьмем число 43₈.
Делим последовательно 4 на 2 и получаем остатки 0,0,1. Записываем их в обратном порядке. Получаем 100.
Делим последовательно 3 на 2 и получаем остатки 1,1. Записываем их в обратном порядке и дополняем ведущими нулями до трех разрядов. Получаем 011.
Записываем вместе и получаем 100011₂

Способ 2:

Используем таблицу триад:

Цифра	1	2	3	4	5	6	7
Триада	000	001	010	011	100	101	110	111

Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.

351₈ = (011) (101) (001) = 011101001₂ = 11101001₂

Как заменить арабские номера месяцев на кварталы римскими цифрами

Пример 2. В таблице Excel содержатся данные о транзакциях компании за каждый месяц в году. Заполнить колонку «Номера отчетных периодов» соответствующими номерами месяцев с использованием римских чисел.

Вид исходной таблицы:

Для вычислений используем следующую формулу массива:

Выражение МЕСЯЦ(ДАТАЗНАЧ(A3:A14&»1″)) возвращает значение номера месяца в виде арабского числа для каждого месяца, которое в свою очередь преобразует в римское число функция РИМСКОЕ. Результат вычислений:

Теперь усложним задачу. Необходимо проставить римскими цифрами номера кварталов соответственно для каждого месяца в году. Для этого добавим в формулу функцию ВЫБОР со своими аргументами: