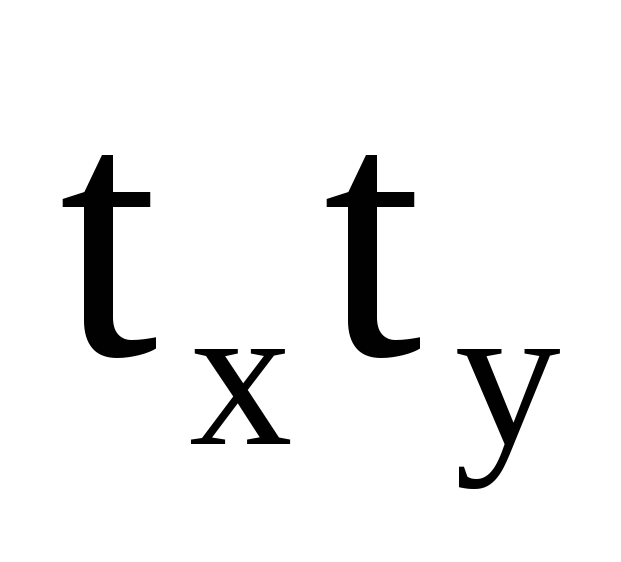Метод корреляционного анализа: пример. корреляционный анализ

Трехмерное представление диаграммы разброса (рассеивания)

Помимо традиционного 2D-представления диаграммы разброса в настоящее время используется 3D-отображение графического представления корреляционного анализа.

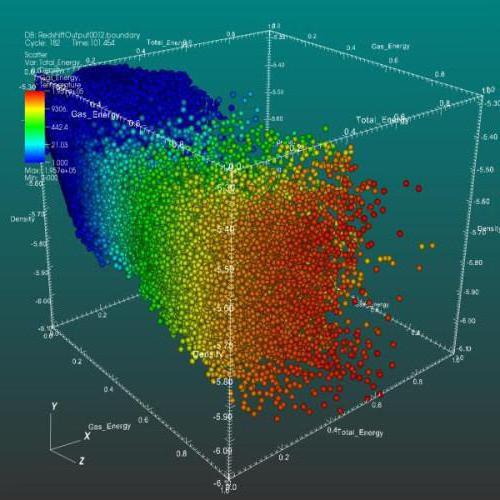
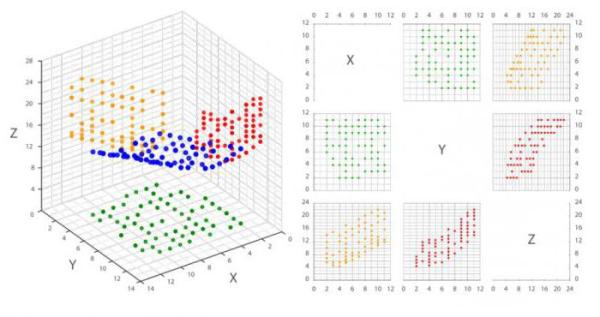
Также используется матрица диаграммы рассеивания, которая отображает все парные графики на одном рисунке в матричном формате. Для n переменных матрица содержит n строк и n столбцов. Диаграмма, расположенная на пересечении i-ой строки и j-ого столбца, представляет собой график переменных Xi по сравнению с Xj. Таким образом, каждая строка и столбец являются одним измерением, отдельная ячейка отображает диаграмму рассеивания двух измерений.

Нелинейные системы

Следует соблюдать осторожность при использовании взаимной корреляции для нелинейных систем. В определенных обстоятельствах, которые зависят от свойств входа, взаимная корреляция между входом и выходом системы с нелинейной динамикой может быть полностью закрыта для определенных нелинейных эффектов

Эта проблема возникает из-за того, что некоторые квадратичные моменты могут равняться нулю, и это может неверно предполагать, что существует небольшая «корреляция» (в смысле статистической зависимости) между двумя сигналами, хотя на самом деле два сигнала сильно связаны нелинейной динамикой.

Какую профессию выбрать девушке

Выбор специализации зависит от множества субъективных факторов, присущих любому человеку. Для женщин ключевыми особенностями при выборе направления деятельности являются:

1. Возраст. В этом случае большое влияние оказывает закон: несовершеннолетним сложнее найти работу даже при наличии официального разрешения от родителей. Совсем юных девушек берут неохотно, потому что у них нет опыта трудовой деятельности. До определенного возраста (до 22-25 лет) стоит рассмотреть должность официантки, проводницы, секретаря.
2. Склад характера, образ мышления. Не все представительницы прекрасного пола являются яркими эмпатами. Это означает, что работа внутри большого коллектива может быть им в тягость. Замкнутым, спокойным девушкам подойдут должности швеи, инженера-оператора, IT-специалиста, работа, связанная с компьютером. Более открытым — профессии актрисы, певицы, теле- или радиоведущей, стилиста, менеджера по туризму.
3. Опыт работы, наличие образования. Человеку с большим стажем не составит труда сменить одну должность на другую: работодатели всегда готовы принять человека, хорошо разбирающегося в своей работе. Человек без опыта — другое дело. Сразу после школы, без опыта, образования девушка может устроиться моделью, горничной, официанткой, секретарем, сиделкой.

После 11 класса

Полное среднее образование даст продолжить обучение в максимально возможном количестве учебных заведений и выбрать самую интересную будущую специальность:

• Медицинские вузы. Московский Государственный медицинский университет (МГМУ) им. И.М. Сеченова, Российский национальный медицинский исследовательский университет (РНИМУ) им. Н.И. Пирогова – медсестра, врач, фармацевт.
• Технические вузы. Московский инженерно-физический институт (МИФИ), Российский химико-технологический университет (РХТУ) им. Д.И. Менделеева, Московский автодорожный институт (МАДИ) – оператор станка, машинист, химик-технолог, инженер-конструктор.
• Гуманитарные, юридические вузы.Московский государственный институт международных отношений (МГИМО), Санкт-Петербургский государственный университет (СПбГУ), Московский независимый эколого-политологический университет (МНЭПУ) – юрист-консультант, адвокат, бухгалтер, экономист.

После 9 класса

Получение неполного среднего образования накладывает свои ограничения на список мест возможного дальнейшего обучения девочек и парней:

• Колледжи. Технические, поварские, специальные.
• Курсы. Парикмахера, маляра, машиниста спец. техники, горничной.

Идеи бизнеса для девушки

Открытие собственного бизнеса или в качестве партнера является неплохим примером удачного начала карьеры. Следующие идеи могут принести девушке успех:

• Торговый представитель косметических компаний (Avon, Amway);
• парикмахерский салон;
• ведение бьюти-блога на youtube;
• школа танцев;
• творческая студия для детей;
• hand-made студия.

Отображение результатов

Результаты корреляционного анализа могут быть представлены в текстовом и графическом видах. В первом случае они представляются как коэффициент корреляции, во втором — в виде диаграммы разброса.

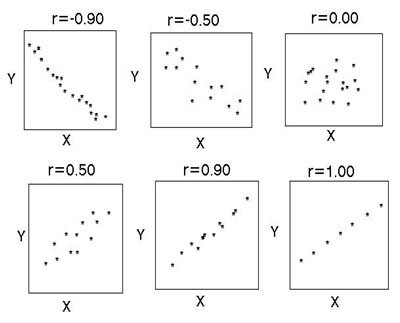
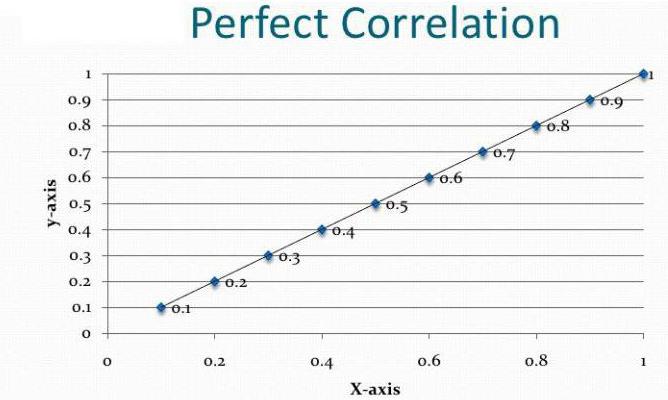
При отсутствии корреляции между параметрами точки на диаграмме расположены хаотично, средняя степень связи характеризуется большей степенью упорядоченности и характеризуется более-менее равномерной удаленностью нанесенных отметок от медианы. Сильная связь стремится к прямой и при r=1 точечный график представляет собой ровную линию. Обратная корреляция отличается направленностью графика из левого верхнего в нижний правый, прямая — из нижнего левого в верхний правый угол.

Проблемы применения

В основе корреляционно-регрессионного анализа лежат следующие предположения:

• Наблюдения считаются независимыми (пятикратное выпадение «орла» никак не влияет на результат следующего подбрасывания монетки).
• В корреляционном анализе обе переменные рассматриваются как случайные. В регрессионном – только одна (зависимая).
• При проверке гипотезы должно соблюдаться нормальное распределение. Изменение зависимой переменной должно быть одинаковым для каждой величины на оси абсцисс.
• Корреляционная диаграмма – это только первая проверка гипотезы о взаимоотношениях между двумя рядами параметров, а не конечный результат анализа.

Что стоит знать?

Право на компенсационные выплаты утрачивается, если в последующем ухаживающему лицу назначают другой вид выплат. Либо, если сам инвалид получает официальную работу. Есть и другие основания, позволяющие прекратить перечисления денежных средств:

1. Пенсионера помещают на государственное обеспечение и содержание, в полном объёме.
2. Уход фактически приостановлен, либо прекращён.
3. Умер сам инвалид, либо тот, кто осуществлял уход.
4. Закончился срок назначения той или иной группы инвалидности. Обычно речь идёт о первой.
5. Лишение родительских прав кровных родственников, которые раньше осуществляли уход.

После наступления самого обстоятельства лицо, осуществляющее уход, должно сообщить об этом в территориальное отделение, не позднее, чем через пять дней. Если сообщение не поступает, то орган власти имеет право потребовать компенсации. В том числе, с использованием судебного порядка разрешения споров.

Отдельное заявление подаётся по новому месту жительства, если прежний адрес проживания инвалида был изменён, но фактический уход за ним продолжается. Можно потребовать возмещения сумм, которые не были выплачены ранее. Но максимум они начисляются за три года, которые предшествовали обращению.

Профессии, не требующие длительной подготовки

Есть женские профессии с низким уровнем стресса, для которых не обязательно учиться несколько лет:

1. Гардеробщица. Что может быть проще, чем принимать и отдавать верхнюю одежду? Правда, у данной работы два существенных минуса: скудная зарплата и необходимость отдыхать все лето;
2. Заводчица собак. Разводить дорогие породы собак хлопотное, но выгодное дело. Собственно, некоторые девушки даже не считают это работой. Для многих это скорее хобби, которое к тому же приносит деньги. Общаться придется лишь с клиентами, которые хотят приобрести элитную породу собак. К тому же животные обожают свою хозяйку и дарят ей множество положительных эмоций;
3. Архивариус. Работа с архивами на крупных предприятиях не особо сложна, но потребует от девушки иногда применять физическую силу. Ведь, чтобы найти нужные документы, порой придется переложить несколько десятков тяжелых папок. К тому же постоянное вдыхание пыли на полках не принесет пользы здоровью. Зато архивариусом мало интересуется начальство, поэтому в целом это весьма спокойная профессия, требующая лишь определенной доли внимательности и аккуратности.

11.4. Коэффициенты прямолинейной парной корреляции

Если взаимосвязь
между изучаемой парой признаков
выражается в форме, близкой к прямолинейной,
то степень тесноты связи между этими
признаками можно рассчитать при помощи
коэффициента
прямолинейной парной корреляции.
В настоящее время имеется много различных
способов расчета коэффициента парной
корреляции. Каждый способ учитывает
характер и особенности взаимосвязей
между изучаемыми признаками в
статистической совокупности. Доказано,
что наиболее точный результат
корреляционной тесноты связи между
факторным и результативным признаками
может быть получен по формуле

,
(11.2)

где r
_ху
– коэффициент парной корреляции между
признаком-фактором (х) и признаком-результатом
(у); t_x
– нормированное отклонение по
признаку-фактору; t
_y
– нормированное отклонение по
признаку-результату.

Коэффициенты
корреляции, также как и корреляционные
отношения, обладают стабильным свойством,
заключающимся в том, что пределы колебаний
этих показателей могут быть выражены
следующим образом: -1< r
_ху
< 1. Это означает, что коэффициенты
корреляции и корреляционные отношения
могут колебаться в пределах, не превышающих
единицу.

Сокращенный
вариант расчета коэффициента парной
корреляции между урожайностью сена
многолетних трав и годовым удоем коров
в 100 сельскохозяйственных организациях
по формуле 11.3 приведен в табл. 11.1.

Т
а б л и ц а 11.
1. Расчет
вспомогательных показателей для
определения коэффициента парной
корреляции

№ п.п.	х, ц/га	, ц/га		, ц/га	у, ц	, ц		, ц
1	20	-10	100	-1,0	20	-15	225	-1,5	1,5
2	21	-9	81	-0,9	20	-15	225	-1,5	1,4
3	22	-8	64	-0,8	25	10	100	-1,0	0,8
…	…	..	…	…	…	…	…	…	…
100	50	20	400	2,0	50	15	225	1,5	3,0
Σ	3000	—	10000	—	3500	—	10000	—	70,0
Среднее	30	—		—	35	—		—	0,7

Как
видно, полученное среднее произведение
нормированных отклонений по признаку-фактору
и признаку-результату
представляет
собой коэффициент парной корреляции
между этими признаками. Поскольку этот
коэффициент положительный, то взаимосвязь
между признаками прямая, а величина
коэффициента корреляции (r
= 0,7) указывает на среднюю меру зависимости
годового удоя одной коровы от урожайности
сена многолетних трав.

Необходимо
иметь в виду, что абсолютная величина
коэффициента корреляции, как и
корреляционного отношения, может
колебаться от 0 до 1, а с учетом направления
связи
– находиться
в пределах от –
1
до 1. При этом чем ближе коэффициент
корреляции к единице (отрицательной
или положительной), тем теснее находятся
признаки во взаимосвязи.

Расчет
коэффициента корреляции по основной
формуле 11.2 хотя и дает довольно точный
результат, но отличается повышенной
трудоемкостью вычисления. Поэтому для
измерения степени тесноты связи между
факторным и результативным признаками
можно рекомендовать формулу, предложенную
К. Пирсоном:

,

(11.3)

где
r
_xy
– коэффициент прямолинейной парной
корреляции;
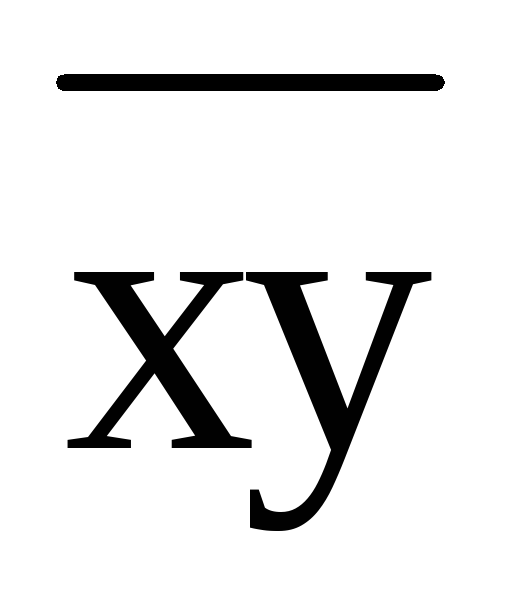– среднее произведение факторного и
результативного признаков: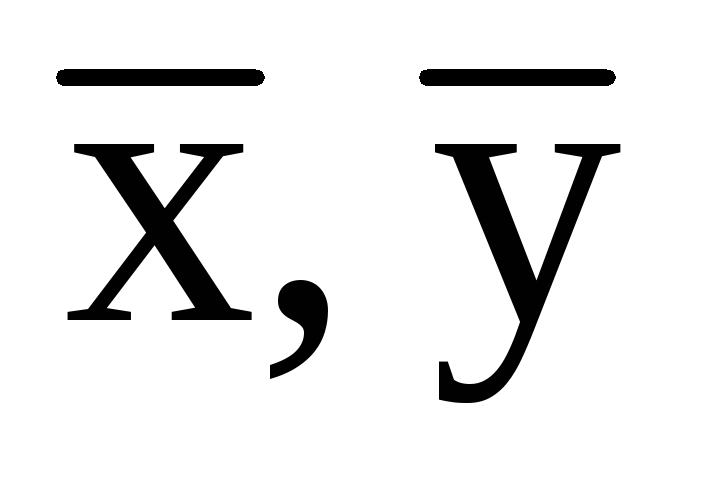– среднее значение соответственного
факторного и результативного признаков,–– средние квадратические отклонения
признака-фактора и признака-результата.

При
расчете коэффициента прямолинейной
парной корреляции по формуле 11.3 в общем
виде можно воспользоваться макетом
вспомогательной табл. 11.2.

Т а б
л и ц а 11.2. Схема
расчета вспомогательных показателей

Памятка

1. Корреляция – это соотношение, взаимозависимость нескольких переменных.
2. Связь бывает положительной и отрицательной.
3. Коэффициент корреляции определяет степень взаимозависимости одной переменной от другой.
4. На основании корреляции люди выдвигают гипотезы (часто ошибочные).
5. Истинная причина корреляции порою скрыта под множеством факторов и внешних сил.
6. Бывает ложная корреляционная зависимость.
7. Раскладывая яйца по корзинам, помните о том, что они не должны коррелироваться друг с другом.

Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru

Использую для заработка

Расчет коэффициента корреляции

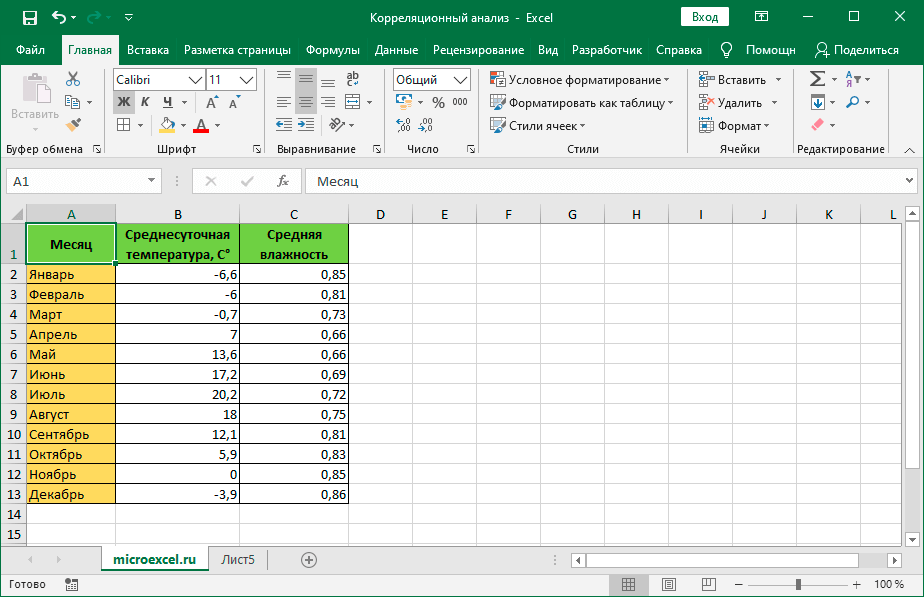
Теперь давайте попробуем посчитать коэффициент корреляции на конкретном примере. Имеем таблицу, в которой помесячно расписана в отдельных колонках затрата на рекламу и величина продаж. Нам предстоит выяснить степень зависимости количества продаж от суммы денежных средств, которая была потрачена на рекламу.

Способ 1: определение корреляции через Мастер функций

Одним из способов, с помощью которого можно провести корреляционный анализ, является использование функции КОРРЕЛ. Сама функция имеет общий вид КОРРЕЛ(массив1;массив2).

1. Выделяем ячейку, в которой должен выводиться результат расчета. Кликаем по кнопке «Вставить функцию», которая размещается слева от строки формул.

В списке, который представлен в окне Мастера функций, ищем и выделяем функцию КОРРЕЛ. Жмем на кнопку «OK».

Открывается окно аргументов функции. В поле «Массив1» вводим координаты диапазона ячеек одного из значений, зависимость которого следует определить. В нашем случае это будут значения в колонке «Величина продаж». Для того, чтобы внести адрес массива в поле, просто выделяем все ячейки с данными в вышеуказанном столбце.

В поле «Массив2» нужно внести координаты второго столбца. У нас это затраты на рекламу. Точно так же, как и в предыдущем случае, заносим данные в поле.

Жмем на кнопку «OK».

Как видим, коэффициент корреляции в виде числа появляется в заранее выбранной нами ячейке. В данном случае он равен 0,97, что является очень высоким признаком зависимости одной величины от другой.

Способ 2: вычисление корреляции с помощью пакета анализа

Кроме того, корреляцию можно вычислить с помощью одного из инструментов, который представлен в пакете анализа. Но прежде нам нужно этот инструмент активировать.

1. Переходим во вкладку «Файл».

В открывшемся окне перемещаемся в раздел «Параметры».

Далее переходим в пункт «Надстройки».

В нижней части следующего окна в разделе «Управление» переставляем переключатель в позицию «Надстройки Excel», если он находится в другом положении. Жмем на кнопку «OK».

В окне надстроек устанавливаем галочку около пункта «Пакет анализа». Жмем на кнопку «OK».

После этого пакет анализа активирован. Переходим во вкладку «Данные». Как видим, тут на ленте появляется новый блок инструментов – «Анализ». Жмем на кнопку «Анализ данных», которая расположена в нем.

Открывается список с различными вариантами анализа данных. Выбираем пункт «Корреляция». Кликаем по кнопке «OK».

Открывается окно с параметрами корреляционного анализа. В отличие от предыдущего способа, в поле «Входной интервал» мы вводим интервал не каждого столбца отдельно, а всех столбцов, которые участвуют в анализе. В нашем случае это данные в столбцах «Затраты на рекламу» и «Величина продаж».

Параметр «Группирование» оставляем без изменений – «По столбцам», так как у нас группы данных разбиты именно на два столбца. Если бы они были разбиты построчно, то тогда следовало бы переставить переключатель в позицию «По строкам».

В параметрах вывода по умолчанию установлен пункт «Новый рабочий лист», то есть, данные будут выводиться на другом листе. Можно изменить место, переставив переключатель. Это может быть текущий лист (тогда вы должны будете указать координаты ячеек вывода информации) или новая рабочая книга (файл).

Когда все настройки установлены, жмем на кнопку «OK».

Так как место вывода результатов анализа было оставлено по умолчанию, мы перемещаемся на новый лист. Как видим, тут указан коэффициент корреляции. Естественно, он тот же, что и при использовании первого способа – 0,97. Это объясняется тем, что оба варианта выполняют одни и те же вычисления, просто произвести их можно разными способами.

Как видим, приложение Эксель предлагает сразу два способа корреляционного анализа. Результат вычислений, если вы все сделаете правильно, будет полностью идентичным. Но, каждый пользователь может выбрать более удобный для него вариант осуществления расчета.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Hard Reset средствами самой системы Android

Корреляция и диверсификация

Как знания о корреляции активов могут помочь лучше вкладывать деньги? Думаю, вы все хорошо знакомы с золотым правилом инвестора — не клади все яйца в одну корзину. Речь, естественно, идёт о диверсификации инвестиционных активов в портфеле. Корреляция и диверсификация неразрывно связаны, что понятно даже из названия — английское diversify означает «разнообразить», а как коэффициент корреляции как раз показывает схожесть или различие двух явлений.

Другими словами, инвестировать в финансовые инструменты с высокой корреляцией не очень хорошо. Почему? Все просто — похожие активы плохо диверсифицируются. Вот пример портфеля двух активов с корреляцией +1:

Как видите, график портфеля во всех деталях повторяет графики каждого из активов — рост и падение обоих активов синхронны. Диверсификация в теории должна снижать инвестиционные риски за счёт того, что убытки одного актива перекрываются за счёт прибыли другого, но здесь этого не происходит совершенно. Все показатели просто усредняются:

Портфель даёт небольшой выигрыш в снижении рисков — но только по сравнению с более доходным Активом 1. А так, никаких преимуществ по сути нет, нам лучше просто вложить все деньги в Актив 1 и не париться.

А вот пример портфеля двух активов с корреляцией близкой к 0:

Где-то графики следуют друг за другом, где-то в противоположных направлениях, какой-либо однозначной связи не наблюдается. И вот здесь диверсификация уже работает:

Мы видим заметное снижение СКО, а значит портфель будет менее волатильным и более стабильно расти. Также видим небольшое снижение максимальной просадки, особенно если сравнивать с Активом 1. Инвестиционные инструменты без корреляции достаточно часто встречаются и из них имеет смысл составлять портфель.

Впрочем, это не предел. Наиболее эффективный инвестиционный портфель можно получить, используя активы с корреляцией -1:

Уже знакомое вам «зеркало» позволяет довести показатели риска портфеля до минимальных:

Несмотря на то, что каждый из активов обладает определенным риском, портфель получился фактически безрисковым. Какая-то магия, не правда ли? Очень жаль, но на практике такого не бывает, иначе инвестирование было бы слишком лёгким занятием.

Корреляционно-регрессионный анализ: параметры созданной модели

Самыми главными факторами, определяющими характеристики модели, принято считать:

• Коэффициенты парной корреляции (демонстрируют силу взаимосвязи двух факторов).
• Коэффициент множественной корреляции (определяет взаимосвязь результата и факторов).
• Коэффициенты частной детерминации (показывают влияние вариации аргумента на вариацию искомого признака).
• Коэффициент множественной детерминации (показывает удельный вес всех аргументов на вариацию искомого признака).
• Частные коэффициенты эластичности (характеризуют влияние факторов на результат, выраженное в едином масштабе в процентах).

Резюме

Особенность киви состоит в том, что данная платежная система не требует при регистрации паспортные данные или какие-либо документы, подтверждающие личность владельца аккаунта. Это предоставляет клиентам платежки возможность оставаться анонимами при выполнении тех или иных переводов, но в этом случае у вас минимальные лимиты в системе. При этом разработана разносторонняя система защиты денежных средств пользователей. Те, кого анонимность не привлекает, могут идентифицировать свою страницу и таким образом увеличить лимит.

Пользователей платежной системы не может не радовать отсутствие комиссии на многие операции и широкий спектр возможностей, который открывается перед участниками программы Qiwi.

 566 

Сфера использования понятия

Корреляция широко распространена в разных видах деятельности с целью обработки массивов статистических данных. Это касается, прежде всего, таких наук, как:

• экономика;
• математика;
• астрофизика;
• психология;
• социология и др.

Отдельно стоит выделить возможность применения корреляции в некоторых важных для человечества сферах деятельности. Это касается металловедения, агрохимии, биометрического анализа и биологии. В разных типах прикладных отраслей принято использовать предельные границы интервалов для оценки тесноты или же значимости связи.

Распространение использования метода корреляции обусловлено такими факторами, как:

• простота подсчета;
• отсутствие необходимости наличия специальной подготовки.

Интерпретация корреляции тоже под силы практически любому человеку. Именно поэтому данный метод так широко используется в различных сферах, где требуется анализ тех или иных статистических данных.

Взаимная корреляция случайных векторов

Определение

Для случайных векторов и , каждый из которых содержит случайные элементы , чьи ожидаемое значение и дисперсию существует, кросс-корреляционная матрица из и определяются
Иксзнак равно(Икс1,…,Иксм)Т{\ Displaystyle \ mathbf {X} = (X_ {1}, \ ldots, X_ {m}) ^ {\ rm {T}}}Yзнак равно(Y1,…,Yп)Т{\ Displaystyle \ mathbf {Y} = (Y_ {1}, \ ldots, Y_ {n}) ^ {\ rm {T}}}Икс{\ displaystyle \ mathbf {X}}Y{\ displaystyle \ mathbf {Y}}

рИксY≜ E⁡ИксYТ{\ displaystyle \ operatorname {R} _ {\ mathbf {X} \ mathbf {Y}} \ треугольник \ \ operatorname {E} }

( Уравнение 3 )

и имеет размеры . Написано покомпонентно:
м×п{\ Displaystyle м \ раз п}

рИксYзнак равноE⁡Икс1Y1E⁡Икс1Y2⋯E⁡Икс1YпE⁡Икс2Y1E⁡Икс2Y2⋯E⁡Икс2Yп⋮⋮⋱⋮E⁡ИксмY1E⁡ИксмY2⋯E⁡ИксмYп{\ displaystyle \ operatorname {R} _ {\ mathbf {X} \ mathbf {Y}} = {\ begin {bmatrix} \ operatorname {E} & \ operatorname {E} & \ cdots & \ operatorname {E} \\\\\ имя оператора {E} & \ operatorname {E} & \ cdots & \ operatorname {E} \\\\\ vdots & \ vdots & \ ddots & \ vdots \\\ \\ operatorname {E} & \ operatorname {E} & \ cdots & \ operatorname {E} \ end {bmatrix}}}

Случайные векторы и не обязательно должны иметь одинаковую размерность, и любой из них может быть скалярным значением.
Икс{\ displaystyle \ mathbf {X}}Y{\ displaystyle \ mathbf {Y}}

пример

Например, если и являются случайными векторами, то
это матрица, -я запись которой равна .
Иксзнак равно(Икс1,Икс2,Икс3)Т{\ displaystyle \ mathbf {X} = \ left (X_ {1}, X_ {2}, X_ {3} \ right) ^ {\ rm {T}}}Yзнак равно(Y1,Y2)Т{\ displaystyle \ mathbf {Y} = \ left (Y_ {1}, Y_ {2} \ right) ^ {\ rm {T}}}рИксY{\ displaystyle \ operatorname {R} _ {\ mathbf {X} \ mathbf {Y}}}3×2{\ displaystyle 3 \ times 2}(я,j){\ displaystyle (я, j)}E⁡ИксяYj{\ displaystyle \ operatorname {E} }

Определение сложных случайных векторов

Если и являются комплексными случайными векторами , каждый из которых содержит случайные величины, ожидаемое значение и дисперсия которых существуют, матрица взаимной корреляции и определяется как
Zзнак равно(Z1,…,Zм)Т{\ Displaystyle \ mathbf {Z} = (Z_ {1}, \ ldots, Z_ {m}) ^ {\ rm {T}}}Wзнак равно(W1,…,Wп)Т{\ Displaystyle \ mathbf {W} = (W_ {1}, \ ldots, W_ {n}) ^ {\ rm {T}}}Z{\ displaystyle \ mathbf {Z}}W{\ displaystyle \ mathbf {W}}

рZW≜ E⁡ZWЧАС{\ displaystyle \ operatorname {R} _ {\ mathbf {Z} \ mathbf {W}} \ треугольник \ \ operatorname {E} }

где обозначает эрмитово транспонирование .
ЧАС{\ displaystyle {} ^ {\ rm {H}}}

Множественная корреляция, её коэффициент

Множественная корреляция — это вероятностная зависимость между одной величиной с
одной стороны, и одновременно несколькими другими ,
с другой стороны.
То есть, в отличие от парной корреляции, при которой
на изменения зависимой (результирующей) переменной влияет одна независимая (объясняющая) переменная,
при множественной корреляции независимых (объясняющих) переменных две или больше.

Цель корреляционного анализа в случае множественной корреляции — установить, есть ли зависимость между
переменными и насколько тесно связаны между собой зависимая переменная, с одной стороны, и независимые
переменные, с другой стороны, и зависят ли друг от друга независимые переменные .

Для того чтобы можно было бы применять модель множественной линейной регрессии, прежде, при анализе
множественной корреляции должны быть установлены следующие факты:

• зависимая переменная тесно зависит от независимых переменных (тесноту связи, как и в случае
  парной корреляции, показывают );
• нет тесной зависимости между независимыми переменными.

Коэффициент множественной корреляции в случае двухфакторной корреляции рассчитывается по следующей формуле:

.

Коэффициенты множественной корреляции между зависимой переменной
и независимыми переменными
записываются в корреляционную матрицу:

Пример 1. Аналитик предприятия решил проверить факторы, которые
влияют на размер заработной платы сотрудников . Предварительно
в качестве объясняющих факторов выбраны: возраст сотрудника ,
стаж работы , оценка теста для приёма
на работу и число подчинённых
сотрудников . Случайно были выбраны
200 сотрудников, данные которых были обобщены. В результате была получена следующая корреляционная матрица:

	1
	-0,27	1
	0,78	-0,63	1
	-0,83	0,47	-0,89	1
	0,65	-0,46	0,17	-0,21	1

Установить, какие переменные можно выбрать как независимые, для того, чтобы далее
можно было бы строить модель множественной регрессии.

Решение.

Корреляционная матрица показывает, что между переменными:

• и — слабая линейная связь: -0,27;
• и — средне тесная положительная линейная связь: 0,78;
• и — тесная отрицательная линейная связь: -0,83;
• и — средне тесная линейная связь: 0,65;
• и — тесная отрицательная линейная связь: -0,89;
• и — слабая линейная связь: 0,17;
• и — слабая линейная связь: -0,21.

Таким образом, не следует включать в число переменных, влияющих на размер заработной
платы возраст сотрудников . Так как
между независимыми переменными и
установлена тесная отрицательная связь,
не включаем в число переменных, влияющих на размер заработной платы стаж работы .
Выбираем в качестве независимых переменных оценку теста для приёма
на работу и число подчинённых
сотрудников .

Чтобы установить тесноту связи между заработной платой сотрудников ,
с одной стороны, и оценкой теста для приёма
на работу и числом подчинённых
сотрудников , с другой стороны,
вычислим коэффициент множественной (двухфакторной) корреляции:

Таким образом, между заработной платой сотрудников, с одной стороны, и
оценкой теста для приёма на работу и числом подчинённых, с другой стороны, существует тесная линейная
связь.

Как показывает пример выше, в исследованиях поведения человека,
как и во многих других направлениях, важно установить, какие факторы из многих действительно влияют на
результат при учете влияния всех остальных факторов

Коэффициент корреляции Пирсона

Теперь мы можем понять, почему ковариация с практической точки зрения очень неудобна. Заданная степень корреляции может соответствовать совершенно разным значениям ковариации, потому что диапазон ковариации определяется стандартными отклонениями двух наборов данных.

Таким образом, мы не можем просто сказать о ковариации и ожидать, что наши коллеги поймут важность нашего анализа. Мы должны сообщать о ковариации и стандартных отклонениях, а наиболее разумный способ сделать это – включить стандартные отклонения в корреляционный анализ

Это то, что мы называем коэффициентом корреляции Пирсона:

\(\rho_{X,Y}=\frac{\operatorname{cov}(X,Y)}{SD(X)SD(Y)}\)

где ρ_X,Y – коэффициент корреляции Пирсона для переменных X и Y (ρ – греческое ро в нижнем регистре). Как видите, мы просто применили проверенный временем метод нормализации.

Когда мы делим ковариацию на произведение двух стандартных отклонений, мы нормализуем ковариацию так, чтобы каждая пара наборов данных давала значение в диапазоне . В результате получается легко интерпретируемая мера линейной корреляции, позволяющая проводить прямые сравнения.

Как это часто бывает в статистике, нам необходимо проводить различие между генеральной совокупностью (популяцией) и выборкой. Символ ρ обозначает коэффициент корреляции Пирсона для генеральной совокупности. Когда мы вычисляем корреляцию Пирсона для выборки, мы используем букву r:

\(r_{xy}={\frac {\sum _{i=1}^{N}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}{{\sqrt {\sum _{i=1}^{N}(x_{i}-{\bar {x}})^{2}}}{\sqrt {\sum _{i=1}^{N}(y_{i}-{\bar {y}})^{2}}}}}\)

Обратите внимание, что члены 1/(N-1) сокращаются. Кроме того, вы, возможно, не знакомы с горизонтальной полосой над X и Y: это еще один метод обозначения среднего, он используется специально для среднего значения выборки, а не генеральной совокупности

Среднее значение для генеральной совокупности обозначается символом μ .

Открытие загрузочной флешки через BIOS

Мало только сделать загрузочный флеш-накопитель. Случается так, что система перестаёт работать. В таком случае образ, записанный на флешку, необходимо открыть через настройки BIOS. Независимо от времени выпуска BIOS, названия, находящиеся в нем, остаются практически неизменными.

После того как вы зашли в BIOS, необходимо открыть «Advanced BIOS Features», в которой размещены устройства, в порядке запуска. Например, сначала загружается жесткий диск, при его отказе система обращается к CDROM. Не найдя системы и на нем, она переходит к USB-HDD. Что нам и надо. Поставив на первое место USB-HDD, сохраняем настройки и выходим из BIOS. При перезагрузке появится меню установки ОС. На некоторых современных системных платах существует специальное Boot Menu, войти в которое можно при загрузке ПК, нажимая F8 или F12, в зависимости от фирмы-изготовителя «материнки», где очень просто можно выбрать загрузку ПК с записанного USB-накопителя. При загрузке ОС через BIOS может возникнуть несколько проблем, таких как:

1. Системная плата не может поддерживать загрузку с внешнего устройства. Это возможно при таком случае, когда «материнка» была сделана до 2003 года;
2. Обнаружение некорректной загрузочной флеш-карты. Вероятно, при записи операционной системы были допущены какие-либо ошибки. Проверьте загрузочную флешку на другом ПК;
3. Отключение контроллера USB в BIOS.

Математические основы

Как сказано выше, в КА входит в себя поиск коэффициента корреляции – числа, показывающего наличие и степень связи между отведениями ЭЭГ-сигнала. Выделяют параметрический коэффициент корреляции Пирсона, применяемый, чтобы определить степень взаимосвязи явлений в рядах с нормальным распределением, и непараметрический коэффициент корреляции Спирмена, используемый при обработке данных, распределение которых отличается от нормального. Нахождение коэффициента корреляции Пирсона производится по формуле ниже.

Значение коэффициента корреляции Пирсона варьируется от -1 до +1. Чем меньше его значение по модулю, тем меньше степень взаимосвязи между явлениями, т.е. наиболее явно связь прослеживается при коэффициенте корреляции +1 или -1.

Прямая корреляция (коэффициент корреляции больше 0) свидетельствует о синфазности, нарастающая амплитуда первого сигнала соответствует увеличению амплитуды второго сигнала, и так же при уменьшении. 

Обратная корреляция (коэффициент корреляции меньше 0) – означает, что  сигналы противофазны, т.е. нарастающая амплитуда первого сигнала соответствует уменьшению амплитуды второго сигнала и наоборот.

При значении коэффициента корреляции 0 сигналы асинхронны, т.е. изменение одного сигнала никак не затрагивает показатели второго. Значимость полученного коэффициента оценивают при помощи критерия Стьюдента.

Помимо коэффициента корреляции в этом анализе существует два понятия: авто- и кросскорреляция. Автокорреляционный анализ оценивает устойчивость (повторяемость) амплитудно-частотных параметров активности в заданном отведении. Кросскорреляционый анализ оценивает повторяемость (схожесть) параметров активности в двух выбранных отведениях.

пример

Рассмотрим совместное распределение вероятностей и приведено в таблице ниже.
Икс{\ displaystyle X}Y{\ displaystyle Y}

п⁡(Иксзнак равноИкс,Yзнак равноу){\ displaystyle \ operatorname {P} (X = x, Y = y)}	узнак равно-1{\ displaystyle y = -1}	узнак равно{\ displaystyle y = 0}	узнак равно1{\ displaystyle y = 1}
Иксзнак равно{\ displaystyle x = 0}	{\ displaystyle 0}	13{\ displaystyle 1/3}	{\ displaystyle 0}
Иксзнак равно1{\ displaystyle x = 1}	13{\ displaystyle 1/3}	{\ displaystyle 0}	13{\ displaystyle 1/3}

Для этого совместного распределения предельными распределениями являются:

п⁡(Иксзнак равноИкс)знак равно{13за Иксзнак равно23за Иксзнак равно1{\ displaystyle \ operatorname {P} (X = x) = {\ begin {cases} 1/3 & \ quad {\ text {for}} x = 0 \\ 2/3 & \ quad {\ text {for}} x = 1 \ end {case}}}

п⁡(Yзнак равноу)знак равно{13за узнак равно-113за узнак равно13за узнак равно1{\ displaystyle \ operatorname {P} (Y = y) = {\ begin {cases} 1/3 & \ quad {\ text {for}} y = -1 \\ 1/3 & \ quad {\ text {for}} y = 0 \\ 1/3 & \ quad {\ text {for}} y = 1 \ end {case}}}

Это дает следующие ожидания и отклонения:

μИксзнак равно23{\ displaystyle \ mu _ {X} = 2/3}

μYзнак равно{\ displaystyle \ mu _ {Y} = 0}

σИкс2знак равно29{\ Displaystyle \ sigma _ {X} ^ {2} = 2/9}

σY2знак равно23{\ Displaystyle \ sigma _ {Y} ^ {2} = 2/3}

Следовательно:

ρИкс,Yзнак равно1σИксσYE⁡(Икс-μИкс)(Y-μY)знак равно1σИксσY∑Икс,у(Икс-μИкс)(у-μY)п⁡(Иксзнак равноИкс,Yзнак равноу)знак равно(1-23)(-1-)13+(-23)(-)13+(1-23)(1-)13знак равно{\ displaystyle {\ begin {align} \ rho _ {X, Y} & = {\ frac {1} {\ sigma _ {X} \ sigma _ {Y}}} \ operatorname {E} \\ & = {\ frac {1} {\ sigma _ {X} \ sigma _ {Y}}} \ sum _ {x , y} {(x- \ mu _ {X}) (y- \ mu _ {Y}) \ operatorname {P} (X = x, Y = y)} \\ & = (1-2 / 3) (- 1-0) {\ frac {1} {3}} + (0-2 / 3) (0-0) {\ frac {1} {3}} + (1-2 / 3) (1-0) {\ frac {1} {3}} = 0. \ end {выравнивается}}}
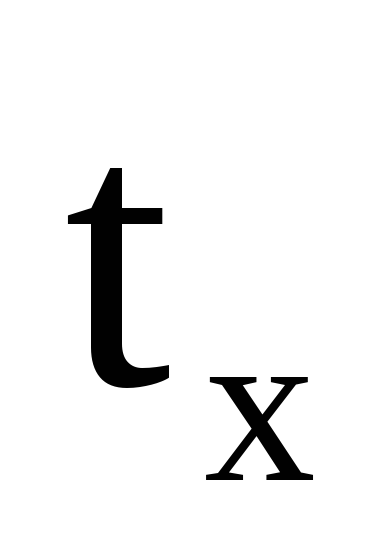
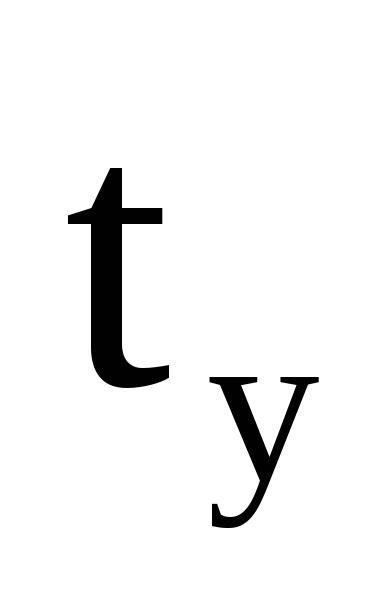