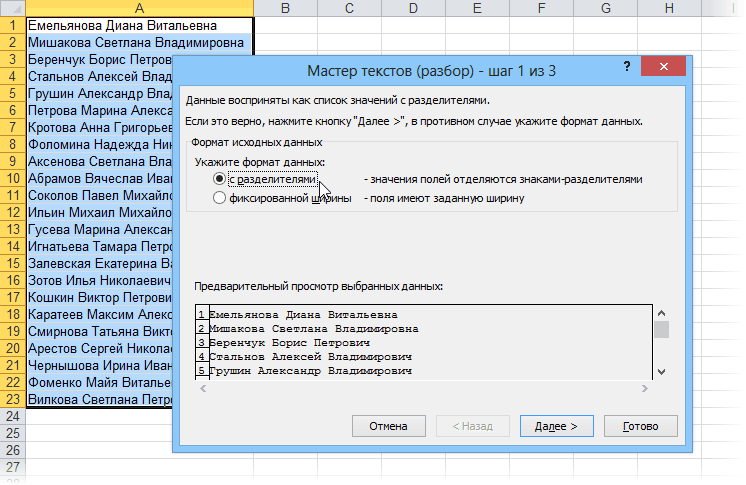
Сложение, вычитание, умножение и деление в excel

Вставка знака умножения в Microsoft Word

Когда нужно поставить знак умножения в MS Word, большинство пользователей выбирают не самое правильное решение. Кто-то ставит “*”, а кто-то поступает еще более радикально, ставя обычную букву “x”. Оба варианта в корне неправильны, хоть и могут “прокатить” в некоторых ситуациях. Если же вы печатаете в Ворде примеры, уравнения, математические формулы, обязательно нужно ставить правильный знак умножения.

Урок: Как в Word вставить формулу и уравнение

Наверное, многие еще со школы помнят, что в различной литературе можно столкнуться с различными обозначениями знака умножения. Это может быть точка, а может быть так называемая буква “x”, с разницей лишь в том, что оба эти символа должны находиться посреди строки и уж точно быть меньше основного регистра. В этой статье мы расскажем о том, как поставить в Ворде знак умножить, каждое из его обозначений.

Урок: Как в Word поставить знак степени

Добавление знака умножения в виде точки

Вы, наверное, знаете о том, что в Ворде имеется довольно большой набор неклавиатурных знаков и символов, которые во многих случаях могут оказаться очень полезными. Мы уже писали об особенностях работы с этим разделом программы, и знак умножения в виде точки мы тоже будем искать там.

Урок: Добавление символов и специальных знаков в Word

Вставка знака через меню “Символ”

1. Кликните в том месте документа, где нужно поставить знак умножения в виде точки, и перейдите во вкладку “Вставка”.

Примечание: Между цифрой (числом) и знаком умножения должен стоять пробел, также пробел должен стоять и после знака, перед следующий цифрой (числом). Как вариант, можно сразу написать те числа, которые нужно перемножить, и сразу поставить между ними два пробела. Знак умножения будем добавлять непосредственно между этими пробелами.

2. Откройте диалоговое окно “Символ”. Для этого в группе “Символы” нажмите кнопку “Символ”, а затем выберите пункт “Другие символы”.

3. В выпадающем меню “Набор” выберите пункт “Математические операторы”.

Урок: Как в Ворде поставить знак суммы

4. В изменившемся списке символов найдите знак умножения в виде точки, кликните по нему и нажмите “Вставить”. Закройте окно.

5. Знак умножения в виде точки будет добавлен в указанном вами месте.

Вставка знака с помощью кода

У каждого знака, представленного в окне “Символ”, есть свой код. Собственно, именно в этом диалоговом окне и можно подсмотреть, какой код имеет знак умножения в виде точки. Там же вы сможете увидеть комбинацию клавиш, которая поможет преобразовать введенный код в знак.

Урок: Горячие клавиши в Word

1. Установите указатель курсора в том месте, где должен находиться знак умножения в виде точки.

2. Введите код “2219” без кавычек. Делать это нужно на цифровом блоке клавиатуры (расположен справа), предварительно убедившись в том, что режим NumLock активен.

3. Нажмите “ALT+X”.

4. Введенные вами цифры будут заменены на знак умножения в виде точки.

Добавление знака умножения в виде буквы “x”

Ситуация с добавлением знака умножения, представленного в виде некоего крестика или, что более близко, уменьшенной буквы “x”, несколько сложнее. В окне “Символ” в наборе “Математические операторы”, как и в других наборах, вы его не найдете. И все же, добавить этот знак можно с помощью специального кода и еще одной клавиши.

Урок: Как в Ворде поставить знак диаметра

1. Установите курсор в том месте, где должен находиться знак умножения в виде крестика. Переключитесь в английскую раскладку.

2. Зажмите клавишу “ALT” и введите на цифровом блоке клавиатуры (справа) код “0215” без кавычек.

Примечание: Пока вы держите клавишу “ALT” и вводите цифры, они не отображаются в строке — так и должно быть.

3. Отпустите клавишу “ALT”, на этом месте появится знак умножения в виде буквы “x”, расположенный посреди строчки, как мы с вами привыкли это видеть в книгах.

Вот, собственно, и все, из этой небольшой статьи вы узнали, как в Word поставить знак умножения, будь то точка или диагональный крестик (буква “x”). Осваивайте новые возможности Ворд и используйте в полной мере потенциал этой программы. Мы рады, что смогли помочь Вам в решении проблемы. Опишите, что у вас не получилось.Наши специалисты постараются ответить максимально быстро.

2.8. Критическая ошибка в Excel 2003

В Excel 2003 функции TREND и
LINEST при определенных
условиях дают неверный результат.

Так происходит когда одновременно:

• среднее значение по каждой переменной в матрице
  предикторов X равно нулю;

• среднее значение отклика Y
  не равно нулю.

На показан как раз такой
случай: средние значения по всем столбцам матрицы Xc
равны нулю, а среднее по столбцу Yc отлично от нуля..

Пример 
 

Рис.37 Ошибка в регрессионных функциях Excel
2003

Ситуацию можно исправить, применяя функцию
TREND к
центрированным значениям отклика, с последующей коррекцией результата.
Для этого можно использовать формулу
=TREND(Yc-ym,
Xc)+ym, применение которой показано на том же рисунке.

Удивительно, но эта ошибка не была замечена
пользователями. Однако в новой версии 2007 она исправлена.  

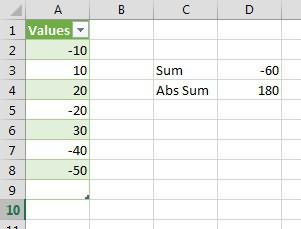
Анализ данных с помощью формулы массива

Формулы массива очень удобно использовать, если стоит задача анализировать информацию. В частности, можно проверять ее на предмет соответствия определенному критерию. Допустим, у нас есть такая таблица, в которой описываются продажи разными менеджерами. В одном отделе работает три сотрудника, а также продается три вида товаров. Ну и наконец, каждый из них имеет свою цену, а итоговая стоимость записывается в третьей колонке таблицы.

17

Перед нами стоит задача определить, насколько каждый из менеджеров является эффективным, учитывая продаваемые ими товары. Это можно сделать и самостоятельно, но с помощью формулы массива данную задачу можно выполнить буквально в несколько кликов. 

Давайте запишем в подходящих ячейках информацию, которая будет служить критерием для оценки эффективности. В нашем случае это товар и идентификатор менеджера, которого мы проверяем.

18

Чтобы успешно решить эту задачу, достаточно просто воспользоваться небольшой формулой массива.

Конечная наша цель – получение суммы, поэтому нужно использовать соответствующую функцию. Кроме этого, нам надо применить условие, на соответствие которым будет проверяться диапазон.

В результате получится формула, приведенная на скриншоте.

19

В ней используется 3 множителя. Первый проверяет менеджеров. Второй – товары. А третий – непосредственно определяет сумму заказа.

Как работает эта формула? Да очень просто. Ее алгоритм следующий:

1. Сначала Excel проверяет всех менеджеров и товары, соответствуют ли они заданным критериям. Если да, функция возвращает значение 1, если нет – 0.

2. В случае несоответствия значений хотя бы одному из условий, один из множителей становится равным нулю. Соответственно, и итоговый результат будет аналогичным.
3. Если же оба условия выполняются, то функция осуществляет операцию умножения.
4. Наконец, все полученные значения суммируются, после чего ячейка выдает общую эффективность по обработанным заказам. 

Вот таким образом можно простую формулу использовать, чтобы выполнять даже самую сложную обработку информации. В конечном итоге, можно несколько модернизировать отчет, добавив выпадающий список, в котором выбираются товары и менеджеры. Но это уже совсем другая тема.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица

3.3. Пример макроса

Второй способ опирается на рекуррентное соотношение,
связывающее два соседних члена в ряду  

Для того чтобы воспользоваться этим соотношением, надо
организовать на листе рекуррентную процедуру. Например, так, как
показано на Рис. 42  

Рис.42 Вычисление функции E₁(x)
итерационным способом

Один шаг итерации – это переход от значений в области
J2:J4 к значениям в области
L2:L4. Для того, чтобы сделать следующую
итерацию, нужно скопировать значения, получившиеся в области
L2:L4 и вставить их в область
J2:J4. При этом вставлять нужно только
величины, без формул. Величины в области H2:H4
дают исходные значения для начала итерации .Повторяя многократно
операцию Copy-Paste Special, можно получить в
ячейке L4 искомое значение. Однако
копирование – это скучное занятие и его было бы неплохо
автоматизировать. Для этого можно написать макрос.

Проще всего начать создание макроса через запись команд,
выполняемых на листе. Для этого идем в раздел меню Tools–Macro–Record
New Macro. Появляется окно (Рис. 43), в котором можно указать имя
макроса и где он будет расположен.  

Рис.43 Запись макро

После нажатия OK начинается
запись всех действий, выполняемых на листе. Когда все, что нужно
сохранено в макросе, запись надо остановить командой
Tools–Macro–Stop Recording. Результат можно увидеть, зайдя в
.   

 

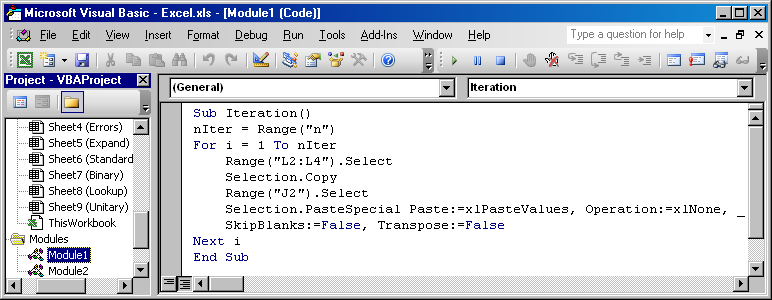
Рис.44 Редактор Visual Basic

На Рис. 44 показан записанный макрос, который мы подвергли
небольшому редактированию – добавили цикл для повтора операции
Copy-Paste в числе nIter
раз. Величина nIter берется со
страницы из ячейки J6,
имеющей локальное имя n. Завершает
автоматизацию кнопка Repeat, к которой
привязан макрос Iteration.  

Такой подход использовался нами для построения
алгоритмов и в многомерном разрешении кривых.

Деление в экселе: как применяется, формула, примеры

Microsoft Office Excel имеет в своем наборе огромную библиотеку функций, которые позволяют проводить анализ числовых данных. Однако программа с легкостью может выступать в роли обычного калькулятора. Для этого в формулы с клавиатуры вставляются базовые математические операции и проводятся вычисления. Сегодня подробнее рассмотрим, как проводить деление в экселе.

Формула и примеры, как делить

Чтобы редактор проводил расчеты, необходимо для начала в активной ячейке поставить знак равно, после этого записать выражение. Сейчас разберем, как сделать деление, и рассмотрим основные варианты использования формулы.

Простые числа

В ячейке после знака равно ставите нужные цифры через знак деления, который на клавиатуре обозначается наклонной чертой. Его можно найти в цифровом блоке или справа от буквы ю на английской раскладке. То есть, чтобы в экселе поставить деление в формулу, достаточно нажать одну кнопку на клавиатуре.

На заметку! Можно одновременно использовать несколько операторов. Последовательность вычислений определена математическими законами: сначала умножение и деление, а потом сложение и вычитание.

Формула будет иметь следующий вид:

Ссылки на ячейки

Аналогичным образом можно использовать адреса ячеек внутри выражения. Тогда нужно четко указывать числитель и знаменатель.

Можно совмещать два предыдущих способа, если, например, знаменатель является неизменным численным значением.

Деление колонки на колонку

Достаточно часто нужно поделить один массив данных на другой. Для этого записываете выражение для одной строки и используете маркер автозаполнения, чтобы формула применялась для всего массива. Например, известна выручка от продажи партии продуктов, а также цена за единицу, необходимо найти количество проданных фруктов.

Решение задачи будет выглядеть следующим образом:

Аналогичным способом выполняется поиск решения, если числитель или знаменатель являются константой. Для этого необходимо зафиксировать значение внутри формулы, то есть сделать абсолютную ссылку на ячейку. Это можно сделать при помощи значка доллара или горячей клавиши F4.

Как известно из математики, провести деление на ноль нельзя. В редакторе также невозможно провести такую операцию. При этом достаточно не только нуля в знаменателе, но и пустой ячейки. Программа выдаст ошибку #ДЕЛ/0.

Функция

Помимо использования пользовательской формулы, в excel есть специальная функция, которая выводит результат в виде целых чисел. Она называется ЧАСТНОЕ. Выражение имеет два известных оператора – числитель и знаменатель.

Однако у этой функции есть одна особенность: в процессе работы округление происходит не по правилам математики, то есть после пяти в большую сторону, а до ближайшего целого. Для сравнения проведем операцию деления простейшей формулой.

Этот момент стоит учитывать при использовании данной функции.

Как видите, делить числа в эксель не сложно. Достаточно знать расположение знака деления на клавиатуре и правильно задать формулу. Если же используете специальную функцию, то помните про округление цифр до ближайшего целого.

Простые операции в Excel: сложение, вычитание

≡  14 Апрель 2016   ·  Рубрика: Могучий MS Excel   

Excel – универсальный инструмент, сложный программный продукт, используемый в различных отраслях.

Но какие-бы сложные инструменты вы не использовали, без простых формул, содержащих элементарные математические операции, вам не обойтись.

Далее я расскажу о том, как делать формулы, содержащие операции сложения и вычитания.

Сложение в Excel – одна из наиболее частых операций, применяемых для создания формул. Рядом со сложением смело можно поставить операцию вычитания. По своему алгебраическому смыслу операции идентичны, но имеют «разный знак». Простейшие алгебраические формулы, которые мы часто видели на школьной доске, выглядят следующим образом.

Простые операции в алгебре

Возможно вы не поверите, но то что вы видели в школе на доске, немногим будет сложнее сделать в Excel. Прежде всего, нужно уяснить, что любая формула в Excel делается по следующим правилам и понятиям:

1. Весь лист разбит на ячейки, и к каждой ячейке можно обратится по адресу. Обычно адрес ячейки выглядит так «А1», «В7». Эти адреса означают, что ячейка находится в столбце А и строке 1 или столбце В и строке 7.
2. Если нужно записать любую формулу, то она записывается в ячейку.
3. В том случае если используются простые операции, тогда, для того, чтобы перейти в режим ввода формулы, нужно поставить знак «=».
4. По завершению ввода формулы нужно нажать «Ввод»
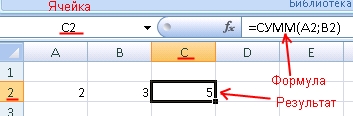
5. В ячейке будет виден результат выполнения формулы, а не сама формула.

Простая операция: сложение, вычитание

Теперь построим формулы сложения и вычитания в Excel.

Допустим: значение А хранится в ячейке «А1», значение В в ячейке В1. В ячейку С1 нужно записать результат суммы А1 и В1, а в ячейке С2 произвести вычитание В1 из А1.

• Формулы сложения и вычитания будут выглядеть так.
• =А1+В1
• =А1-В1

Вид формулы сложения

Вид формулы вычитания

Все четко видно на картинках, хочется только добавить  — не забывайте нажимать Ввод после окончания ввода любой формулы, не обязательно сложения или вычитания. И понятно, что для сложения используется символ «+», для вычитания символ «-».

Сложные варианты сложения: Функция СУММ()

Одним из сложных вариантов является прибавление процентов. Из-за сложности вопроса я написал отдельную статью.

КАК ПРИБАВИТЬ ПРОЦЕНТЫ В EXCEL С ПОМОЩЬЮ ФОРМУЛЫ

Прежде всего, нужно рассмотреть сложение ячеек по столбцу. Наилучший способ использование в формуле функции «СУММ». Этой функции передается диапазон ячеек и/или указываются, через точку с запятой, ячейки, по которым нужно провести суммирование.

Вид задания

Посмотрите на рисунок, условия задачи таковы: в ячейку F6 нужно записать сумму чисел записанных в диапазоне С1:С5, прибавить D1 и прибавить диапазон чисел записанный в D3:D5.

1. Становимся курсором в позицию F6 и нажимаем на кнопку «Вставить функцию».
2. В открывшемся окне «Мастер функций», есть поле поиск функции , в него мы записываем «Сумм»(без кавычек) и нажимаем кнопку «Ок»(в диалоговом окне)!

Мастер функций

После проделанных действий откроется другое диалоговое окно «Аргументы функции».

Теперь для функции сумм нужно установить параметры – диапазоны и ячейки для суммирования

Обращаю внимание, что таких параметров может быть 255 и при ручном вводе разделять их нужно символом «;»

Аргументы функций

После нажатия на кнопке , в ячейке F6 будет записана формула содержащая функцию суммирования, но пользователь увидит результат суммирования.

Думаю, прочитав эту статью, вы убедились, что операции сложения и вычитания это очень просто. Могу лишь посоветовать экспериментировать, экспериментировать и еще …

1.2. Книга, лист и ячейка

Файл Excel с расширением XLS (XLSX в версии 2007) называется
(рабочей) книгой. Если запустить программу Excel, например, щелкнуть на
рабочем столе иконку
,
то откроется новая пустая книга. . 

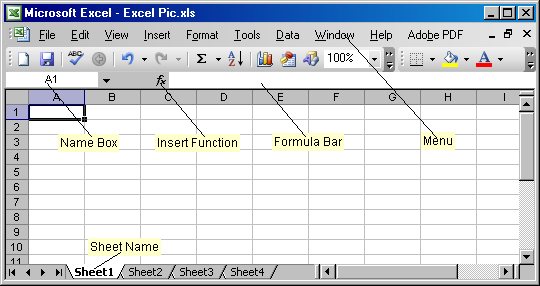
Рис. 2 Новая книга Excel

Если рабочая книга уже существует, то ее проще открыть через проводник. Для
этого достаточно щелкнуть по иконке файла.  

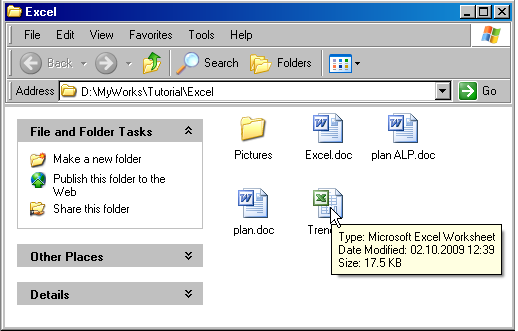
Рис. 3
Открытие книги Excel через проводник

Рабочая книга состоит из нескольких листов, имена которых
показаны в нижней части окна. Листы можно удалять, добавлять,
переименовывать. Для этого надо щелкнуть правой клавишей мышки по имени
листа. Появится меню, из которого можно выбрать нужную операцию.

Рис.
4 Операции с листами

Стандартное имя листа – Sheet1, но ему можно дать любое имя, например
Data. На лист можно вставлять рисунки, графики и другие необходимые
объекты.

Каждый лист состоит из ячеек, образующих таблицу, размером 256
столбцов и 65536 строк (В версии 2007 – 16384 столбцов и1048576 строк).
Строки на листе обозначены числами: 1,2, 3…, а столбцы имеют буквенную
кодировку: A, B, …,Z,
AA, AB .., и т.д. до последнего столбца
IV (в 2007
– до XFD). Этот стиль адресации называется A1. Реже применяется
альтернативный стиль R1C1, в котором столбцы также нумеруются. Мы не
будем использовать этот стиль, а прочитать об этом можно

здесь

Строки и столбцы можно удалять, добавлять, прятать, а также менять их размер:
высоту или ширину.

Все операции на листе выполняются с помощью меню, представленного в
верхней части окна (). Меню в Excel 2007
существенно отличается от прежней версии. Там, вместо обычных иконок,
появилась лента. Мы не будем подробно разбирать отличия версий. Те, кому
это интересно могут прочитать

здесь.

2.7. Регрессия

Для построения используются
несколько стандартных функций листа.

TREND / ТЕНДЕНЦИЯ

Строит

y=b+m₁x₁+…+m_J x_J+e

Аппроксимирует известные значения вектора откликов
known_y’s для заданных значений матрицы предикторов
known_x’s и возвращает значения y,
для заданного массива new_x’s.  

Синтаксис 

TREND(known_y’s
)

Примечания 

• Вектор
  known_y’s должен занимать один столбец,
  тогда каждый столбец матрицы массива known_x’s
  интерпретируется как отдельная переменная;

• Если
  аргумент known_x’sопущен, то предполагается, что это вектор чисел {1;2;3;…}
  такого же размера, как и known_y’s;

• Матрица
  новых значений new_x’sдолжна иметь столько же столбцов
  (переменных), как и матрица known_x’s;

• Если
  аргумент new_x’sопущен, то предполагается, что он совпадает с
  массивом known_x’s.
  Результат является вектором, в котором число строк равно
  числу строк в массиве new_x’s.

Пример 
 

Рис.34 Функция TREND

Функция TRENDявляется функцией
массива и ее ввод должен завершаться нажатием комбинации
CTRL+SHIFT+ENTER. 

LINEST /
ЛИНЕЙН

Дополняет функцию TREND и выводит некоторые
статистические значения, связанные с регрессией  

y=b+m₁x₁+…+m_J x_J+e

Синтаксис 

LINEST(known_y’s
)

 

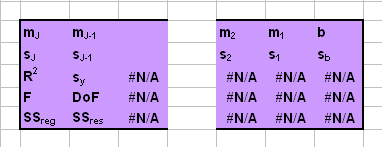
Рис. 35 Таблица вывода функция LINEST

m_J, …,
m₂, m₁
и b – оценки регрессионных
коэффициентов;

s_J, …,
s₂, s₁
и s_b
– стандартные ошибки для оценок регрессионных коэффициентов;

R2 –
коэффициент детерминации;

s_y –
стандартная ошибка оценки y;

F – F-статистика;

DoF – число степеней
свободы;

SS_reg –
регрессионная сумма квадратов;

SS_res–
остаточная сумма квадратов.

Примечания 

• LINEST – это
  очень плохо сконструированная функция, очень неудобная в
  практическом применении;

• Примечания,
  представленные в описании функции полностью применимы к
  функции LINEST.

Пример 
 

Рис.36 Функция LINEST

Функция LINEST является функцией массива и ее ввод должен
завершаться нажатием комбинации CTRL+SHIFT+ENTER. 

Формулы массива в Excel

Под массивом обычно понимают набор данных, объединенных в группу. Массивы бывают одномерные (элементы массива образуют строку или столбец) или двумерные (матрица). Легко сообразить, что почти в любой таблице Excel при желании можно найти один или несколько таких массивов:

Формулы массива в Excel – это специальные формулы для обработки данных из таких массивов. Формулы массива делятся на две категории – те, что возвращают одно значение и те, что дают на выходе целый набор (массив) значений. Рассмотрим их на простых примерах…

Пример 1. Классика жанра – товарный чек

Задача: рассчитать общую сумму заказа. Если идти классическим путем, то нужно будет добавить столбец, где перемножить цену и количество, а потом взять сумму по этому столбцу. Если же применить формулу массива, то все будет гораздо красивее:

1. выделяем ячейку С7
2. вводим с клавиатуры =СУММ(
3. выделяем диапазон B2:B5
4. вводим знак умножения (звездочка)
5. выделяем диапазон C2:C5 и закрываем скобку функции СУММ – в итоге должно получиться так:
6. чтобы Excel воспринял нашу формулу как формулу массива жмем не Enter, как обычно, а Ctrl + Shift + Enter

Вуаля!

Т.е. Excel произвел попарное умножение элементов массивов B2:B5 и C2:C5 и образовал новый массив стоимостей (в памяти компьютера), а затем сложил все элементы этого нового массива.

Обратите внимание на фигурные скобки, появившиеся в формуле – отличительный признак формулы массива. Вводить их вручную с клавиатуры бесполезно – они автоматически появляются при нажатии Ctrl + Shift + Enter

Пример 2. Разрешите Вас… транспонировать?

При работе с таблицами часто возникает необходимость поменять местами строки и столбцы, т.е. развернуть таблицу на бок, чтобы данные, которые раньше шли по строке, теперь располагались в столбцах и наоборот. В математике такая операция называется транспонированием. При помощи формулы массива и функции ТРАНСП (TRANSPOSE) это делается на раз.

Допустим, имеем двумерный массив ячеек, который хотим транспонировать.

• Выделяем диапазон ячеек для размещения транспонированной таблицы. Поскольку исходный массив ячеек был 8 строк на 2 столбца, то надо выделить диапазон пустых ячеек размером 2 строки на 8 столбцов.
• вводим функцию транспонирования =ТРАНСП(   
• в качестве аргумента функции выделяем наш массив ячеек A1:B8

жмем Ctrl + Shift + Enter и получаем “перевернутый массив” в качестве результата:

Редактирование формулы массива

Если формула массива расположена не в одной ячейке (как в Примере 1), а в нескольких ячейках (как в Примере 2), то Excel не позволит редактировать или удалить одну отдельно взятую формулу (например в ячейке D10) и выдаст предупреждающее сообщение Невозможно изменить часть массива.

Для редактирования формулы массива необходимо выделить весь диапазон (A10:H11 в нашем случае) и изменить формулу в строке формул (или нажав F2). Затем необходимо повторить ввод измененной формулы массива, нажав сочетание клавиш Ctrl + Shift + Enter.

Excel также не позволит свободно перемещать ячейки, входящие в формулу массива или добавлять новые строки-столбцы-ячейки в диапазон формулы массива (т.е. в диапазон A10:H11 в нашем случае)

Пример 3. Таблица умножения

Вспомните детство, школу, свою тетрадку по математике… На обороте тетради на обложке было что? Таблица умножения вот такого вида:

При помощи формул массива она вся делается в одно движение:

1. выделяем диапазон B2:K11
2. вводим формулу =A2:A11*B1:K1
3. жмем Ctrl + Shift + Enter, чтобы Excel воспринял ее как формулу массива

и получаем результат:

Пример 4. Выборочное суммирование

Посмотрите как при помощи одной формулы массива красиво и легко выбираются данные по определенному товару и заказчику:

 В данном случае формула массива синхронно пробегает по всем элементам диапазонов C3:C21 и B3:B21, проверяя, совпадают ли они с заданными значениями из ячеек G4 и G5. Если совпадения нет, то результат равенства ноль, если совпадение есть, то единица. Таким образом суммы всех сделок, где заказчик не ANTON и товар не Boston Crab Meat умножаются на ноль и суммируются только нужные заказы.

Учимся программировать

Задание 1. Транспонировать данную матрицу

1. Заполните ячейки таблицы значениями элементов матрицы (рис.1).

Рисунок 1.

Выделите диапазон ячеек (рис.2) – здесь будет располагаться транспонированная матрица.

Рисунок 2.

Вызовите мастер функций (меню Вставка-Функция или значок Вставить функцию в строке формул). В категории «Полный алфавитный перечень» найдите функцию «ТРАНСП» и нажмите ОК.

Рисунок 3.

В появившемся окне введите диапазон значений исходной матрицы.

Рисунок 4.

Для получения результата одновременно нажмите клавиши «Ctrl»+«Shift»+«Enter».

Рисунок 5.

2. Умножение матрицы на числоЗадание 2. Дана матрица А (рис.6). Получить матрицу B=3*А. Ход работы:

1. Введите матрицу (рис.6).
2. Выделите ячейку E1 и введите формулу =3*A1.
3. Скопируйте введенную формулу в остальные ячейки результирующей матрицы: для этого наведите курсор на точку в правом нижнем углу ячейки, так, чтобы курсор изменился на тонкий крестик, нажмите на левую кнопку мыши и протяните до ячейки G1. Таким же образом протяните указатель до ячейки G2.
4. В результате должна получиться матрица B (рис.7):

Рисунок 6. Матрица A

Рисунок 7. Матрица B

3. Сложение матрицЗадание 3. Сложить две матрицы A и B (даны на рис.8).

Рисунок 8.

Ход работы:

1. Введите две матрицы A и B (рис.8).
2. Выделите первую ячейку результирующей матрицы D5 и внесите формулу =B1+F1.
3. Скопируйте формулу на оставшиеся ячейки матрицы C.

Рисунок 9. Результат

Уровень 2

4.Умножение матрицЗадание 4.Даны матрицы А и В (рис.10). Найти их произведение С=А*В.

Рисунок 10.

Ход работы:

1. Выделяем мышкой при нажатой левой кнопке соответствующий диапазон ячеек D5:E7 (строк такое же количество как в матрице А, а столбцов такое же количество как в матрице В).
2. Вызываем мастер функций и в категории «Полный алфавитный перечень находим функцию «МУМНОЖ» и нажимаем ОК.

1. В появившемся окне вводим диапазон значений исходных матриц А и В (рис.11).

Рисунок 11.

1. Для получения результата нажимаем сочетание клавиш «Shift»+«Ctrl»+«Enter».

Рисунок 12

Задание 5. Самостоятельно с помощью функции ТРАНС транспонировать следующую матрицу.

Рисунок 13.

Уровень 3

Задание 6. Самостоятельно выполнить с помощью Excel умножение матриц А и В. Даны А и В. В результате вычислений должна получиться матрица C (рис.14)

Рисунок 14.

Задание 7.  Даны матрицы А, В, С и число a=2. Найти

Подсказка: Все вычисления выполнять на одном листе. Сначала вычислить, затем умножить матрицы , далее умножить матрицу С на число a, затем сложить  матрицы  и aС.Тест: результат Задание 8. Даны матрицы А, В, С и число a=2. Найти

Тест: результат

Вопросы на повторение:

1. Какая функция в Excel используется для транспонирования матрицы?
2. Какая функция в Excel используется для умножения матриц?

Уровень 1

Задание 1: найти произведение матриц AB, где

Задание 2: найти произведение матриц BA, где

Задание 3:  Даны матрицы А, В. Найти

Тест:

Бизнес и финансы

БанкиБогатство и благосостояниеКоррупция(Преступность)МаркетингМенеджментИнвестицииЦенные бумагиУправлениеОткрытые акционерные обществаПроектыДокументыЦенные бумаги — контрольЦенные бумаги — оценкиОблигацииДолгиВалютаНедвижимость(Аренда)ПрофессииРаботаТорговляУслугиФинансыСтрахованиеБюджетФинансовые услугиКредитыКомпанииГосударственные предприятияЭкономикаМакроэкономикаМикроэкономикаНалогиАудитМеталлургияНефтьСельское хозяйствоЭнергетикаАрхитектураИнтерьерПолы и перекрытияПроцесс строительстваСтроительные материалыТеплоизоляцияЭкстерьерОрганизация и управление производством

Основные свойства матричного произведения

В двух словах. Умножение матриц:

1. Некоммутативно: $A\cdot B\ne B\cdot A$ в общем случае. Бывают, конечно, особые матрицы, для которых равенство $A\cdot B=B\cdot A$ (например, если $B=E$ — единичной матрице), но в абсолютном большинстве случаев это не работает;
2. Ассоциативно: $\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)$. Тут без вариантов: стоящие рядом матрицы можно перемножать, не переживая за то, что стоит левее и правее этих двух матриц.
3. Дистрибутивно: $A\cdot \left( B+C \right)=A\cdot B+A\cdot C$ и $\left( A+B \right)\cdot C=A\cdot C+B\cdot C$ (в силу некоммутативности произведения приходится отдельно прописывать дистрибутивность справа и слева.

А теперь — всё то же самое, но более подробно.

Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.

Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:

\\cdot \left=\left\]

Но если поменять матрицы местами, то получим совсем другой результат:

\\cdot \left=\left\]

Получается, что $A\cdot B\ne B\cdot A$. Кроме того, операция умножения определена только для согласованных матриц $A=\left$ и $B=\left$, но никто не гарантировал, что они останутся согласованными, если их поменять местами. Например, матрицы $\left$ и $\left$ вполне себе согласованы в указанном порядке, но те же матрицы $\left$ и $\left$, записанные в обратном порядке, уже не согласованы. Печаль.:(

Тем не менее, умножение матриц ассоциативно:

\

Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.

В реальных задачах чаще всего приходится перемножать квадратные матрицы размера $\left$. Множество всех таких матриц обозначается ${{M}^{n}}$ (т.е. записи $A=\left$ и \ означают одно и то же), и в нём обязательно найдётся матрица $E$, которую называют единичной.

Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:

\

Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)

Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.

Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?

Печь на отработанном масле: варианты изготовления устройства своими руками

Яндекс сколько стоит машина

Trend Micro Internet Security