Массивы (матрицы) в python
Содержание:
- Введение
- Обработка элементов двумерного массива
- 7.3. Статистика
- Транспонирование матрицы
- Выбираем устройство загрузки
- Случайные величины (numpy.random)¶
- ИГУМО и ИТ, Институт гуманитарного образования и информационных технологий
- 7.2. Линейная алгебра
- Runtastic
- Основные понятия и идеи нарративного подхода
- Пакеты в SciPy
- Создание массивов
- Copies and Views¶
- Документация и учебники
- Двумерные массивы
- Навигация по записям
Введение
Импортируйте библиотеку Numpy, если вы еще этого не сделали.
>>> import numpy as np
Для начала создадим матрицу, которая нам понадобится в работе.
>>> m = np.matrix('1 2 3 4; 5 6 7 8; 9 1 5 7')
>>> print(m)
]
В этом случае будет создан объект типа matrix.
>>> type(m) <class 'numpy.matrixlib.defmatrix.matrix'>
Если вы уже работали с Numpy, это может для вас быть чем-то новым. В Numpy, как правило, приходится работать с объектами класса ndarray. Мы выбрали matrix из-за удобства объявления массива, т.к. matrix позволяет использование Matlab-подобный стиль, и, наверное, вам будет интересно познакомиться с чем-то новым. Для задач, рассматриваемых в рамках данной статьи, объекты matrix и ndarray одинаково хорошо подходят. Matix можно превратить в ndarray вот так:
>>> m = np.array(m) >>> type(m) <class 'numpy.ndarray'>
В любом случае наша таблица чисел будет выглядеть следующим образом.
Обработка элементов двумерного массива
Нумерация элементов двумерного массива, как и элементов одномерного массива, начинается с нуля.
Т.е. — это элемент третьей строки четвертого столбца.
Пример обработки элементов матрицы:
Найти произведение элементов двумерного массива.
Решение:
1 2 3 4 5 |
p = 1
for i in range(N):
for j in range(M):
p *= matrixij
print (p)
|
Пример:
Найти сумму элементов двумерного массива.
Решение:
Более подходящий вариант для Python:
1 2 3 4 |
s = for row in matrix: s += sum(row) print (s) |
Для поиска суммы существует стандартная функция sum.
Задание Python 8_0:
Получены значения температуры воздуха за 4 дня с трех метеостанций, расположенных в разных регионах страны:
| Номер станции | 1-й день | 2-й день | 3-й день | 4-й день |
|---|---|---|---|---|
| 1 | -8 | -14 | -19 | -18 |
| 2 | 25 | 28 | 26 | 20 |
| 3 | 11 | 18 | 20 | 25 |
Т.е. запись показаний в двумерном массиве выглядела бы так:
| t:=-8; | t:=-14; | t:=-19; | t:=-18; |
| t:=25; | t:=28; | t:=26; | t:=20; |
| t:=11; | t:=18; | t:=20; | t:=25; |
- Распечатать температуру на 2-й метеостанции за 4-й день и на 3-й метеостанции за 1-й день.
- Распечатать показания термометров всех метеостанций за 2-й день.
- Определить среднюю температуру на 3-й метеостанции.
- Распечатать, в какие дни и на каких метеостанциях температура была в диапазоне 24-26 градусов тепла.
Задание Python 8_1:
Написать программу поиска минимального и максимального элементов матрицы и их индексов.
Задание Python 8_2:
Написать программу, выводящую на экран строку матрицы, сумма элементов которой максимальна.
Для обработки элементов квадратной матрицы (размером N x N):
Для элементов главной диагонали достаточно использовать один цикл:
for i in range(N): # работаем с matrix |
Для элементов побочной диагонали:
for i in range(N): # работаем с matrix |
Пример:Переставить 2-й и 4-й столбцы матрицы. Использовать два способа.
Решение:
-
for i in range(N): c = Ai2 Ai2 = Ai4 Ai4 = c
-
for i in range(N): Ai2, Ai4 = Ai4, Ai2
Задание Python 8_3:
Составить программу, позволяющую с помощью датчика случайных чисел сформировать матрицу размерностью N. Определить:
минимальный элемент, лежащий ниже побочной диагонали;
произведение ненулевых элементов последней строки.
7.3. Статистика
Над данными в массивах можно производить определенные вычисления, однако, не менее часто требуется эти данные как-то анализировать. Зачастую, в этом случае мы обращаемся к статистике, некоторые функции которой тоже имеются в NumPy. Данные функции могут применять как ко всем элементам массива, так и к элементам, расположенным вдоль определенной оси.
Элементарные статистические функции:
Средние значения элементов массива и их отклонения:
Корреляционные коэфициенты и ковариационные матрицы величин:
Так же NumPy предоставляет функции для вычисления гистограмм наборов данных различной размерности и некоторые другие статистичские функции.
Транспонирование матрицы
Транспонирование матрицы – это процесс замены строк матрицы на ее столбцы, а столбцов соответственно на строки. Полученная в результате матрица называется транспонированной. Символ операции транспонирования – буква T.
➣ Численный пример
Для исходной матрицы:
Транспонированная будет выглядеть так:
➤ Пример на Python
Решим задачу транспонирования матрицы на Python. Создадим матрицу A:
>>> A = np.matrix('1 2 3; 4 5 6')
>>> print(A)
]
Транспонируем матрицу с помощью метода transpose():
>>> A_t = A.transpose() >>> print(A_t) ]
Существует сокращенный вариант получения транспонированной матрицы, он очень удобен в практическом применении:
>>> print(A.T) ]
Рассмотрим на примерах свойства транспонированных матриц. Операции сложения и умножение матриц, а также расчет определителя более подробно будут рассмотрены в последующих уроках.
Свойство 1. Дважды транспонированная матрица равна исходной матрице:
➣ Численный пример

➤ Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6')
>>> print(A)
]
>>> R = (A.T).T
>>> print(R)
]
Свойство 2. Транспонирование суммы матриц равно сумме транспонированных матриц:
➣ Численный пример

➤Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6')
>>> B = np.matrix('7 8 9; 0 7 5')
>>> L = (A + B).T
>>> R = A.T + B.T
>>> print(L)
]
>>> print(R)
]
Свойство 3. Транспонирование произведения матриц равно произведению транспонированных матриц расставленных в обратном порядке:
➣ Численный пример

➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> B = np.matrix('5 6; 7 8')
>>> L = (A.dot(B)).T
>>> R = (B.T).dot(A.T)
>>> print(L)
]
>>> print(R)
]
В данном примере, для умножения матриц, использовалась функция dot() из библиотеки Numpy.
Свойство 4. Транспонирование произведения матрицы на число равно произведению этого числа на транспонированную матрицу:
➣ Численный пример
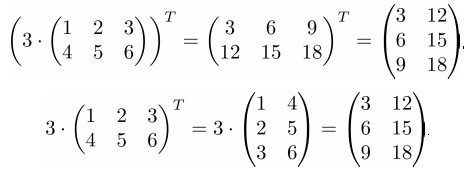
➤ Пример на Python
>>> A = np.matrix('1 2 3; 4 5 6')
>>> k = 3
>>> L = (k * A).T
>>> R = k * (A.T)
>>> print(L)
]
>>> print(R)
]
Свойство 5. Определители исходной и транспонированной матрицы совпадают:
➣ Численный пример
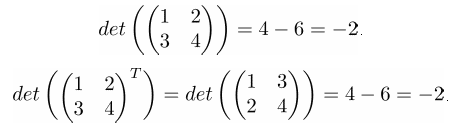
➤ Пример на Python
>>> A = np.matrix('1 2; 3 4')
>>> A_det = np.linalg.det(A)
>>> A_T_det = np.linalg.det(A.T)
>>> print(format(A_det, '.9g'))
-2
>>> print(format(A_T_det, '.9g'))
-2
Ввиду особенностей Python при работе с числами с плавающей точкой, в данном примере вычисления определителя рассматриваются только первые девять значащих цифр после запятой (за это отвечает параметр ‘.9g’).
Выбираем устройство загрузки
Случайные величины (numpy.random)¶
В модуле numpy.random собраны функции для генерации массивов случайных чисел различных распределений и свойств.
Их можно применять для математического моделирования. Функция random() создает массивы из псевдослучайных чисел,
равномерно распределенных в интервале (0, 1). Функция RandomArray.randint() для получения массива равномерно
распределенных чисел из заданного интервала и заданной формы. Можно получать и случайные перестановки с помощью
RandomArray.permutation(). Доступны и другие распределения для получения массива нормально распределенных величин
с заданным средним и стандартным отклонением:
Следующая таблица приводит основные функции модуля.
| Команда | Описание |
|---|---|
| rand(d0, d1, …, dn) | набор случайных чисел заданной формы |
| randn() | набор (или наборы) случайных чисел со стандартным нормальным распределением |
| randint(low) | случайные целые числа от low (включая) до high (не включая). |
| random_integers(low) | случайные целые числа между low и high (включая). |
| random_sample() | случайные рациональные числа из интервала [0.0, 1.0). |
| bytes(length) | случайные байты |
| shuffle(x) | тасовка элементов последовательностина месте |
| permutation(x) | возвращает последовательность, переставленных случайным образом элементов |
| seed() | перезапуск генератора случайных чисел |
| beta(a, b) | числа с Бетта- распределением \(f(x,\alpha,\beta)=\frac{1}{B(\alpha,\beta)}x^{\alpha-1}(1-x)^{\beta-1}\) \(B(\alpha,\beta)=\int_0^1 t^{\alpha-1}(1-t)^{\beta-1}dt\) |
| binomial(n, p) | числа с биномиальным распределением \(P(N)= \left( \frac{n}{N} \right) p^N (1-p)^{n-N}\) |
| chisquare(df) | числа с распределением хи-квадрат \(p(x)=\frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2-1} e^{-x/2}\) |
| mtrand.dirichlet(alpha) | числа с распределением Дирихле (alpha – массив параметров). |
| exponential() | числа с экспоненциальным распределением \(f(x,\frac{1}{\beta})=\frac{1}{\beta}exp(-\frac{x}{\beta})\) |
| f(dfnum, dfden) | числа с F распределением (dfnum – число степеней свободы числителя > 0; dfden –число степеней свободы знаменателя >0.) |
| gamma(shape) | числа с Гамма — распределением |
| geometric(p) | числа с геометрическим распределением |
| gumbel() | числа с распределением Гумбеля |
| hypergeometric(ngood, nbad, nsample) | числа с гипергеометрическим распределением (n = ngood, m = nbad, and N = number of samples) |
| laplace() | числа с распределением Лапласа |
| logistic() | числа с логистическим распределением |
| lognormal() | числа с логарифмическим нормальным распределением |
| logseries(p) | числа с распределением логарифмического ряда |
| multinomial(n, pvals) | числа с мультиномиальным распределением |
| multivariate_normal(mean, cov) | числа с мульти нормальным распределением (mean – одномерный массив средних значений; cov – двухмерный симметричный, полож. определенный массив (N, N) ковариаций |
| negative_binomial(n, p) | числа с отрицательным биномиальным распределением |
| noncentral_chisquare(df, nonc) | числа с нецентральным распределением хи-квадрат |
| noncentral_f(dfnum, dfden, nonc) | числа с нецентральным F распределением (dfnum — целое > 1; dfden – целое > 1; nonc : действительное >= 0) |
| normal() | числа с нормальным распределением |
| pareto(a) | числа с распределением Паретто |
| poisson() | числа с распределением Пуассона |
| power(a) | числа со степенным распределением |
| rayleigh() | числа с распределением Релея |
| standard_cauchy() | числа со стандартным распределением Коши |
| standard_exponential() | числа со стандартным экспоненциальным распределением |
| standard_gamma(shape) | числа с гамма- распределением |
| standard_normal() | числа со стандартным нормальным распределением (среднее=0, сигма=1). |
| standard_t(df) | числа со стандартным распределением Стьюдента с df степенями свободы |
| triangular(left, mode, right) | числа из треугольного распределения |
| uniform() | числа с равномерным распределением |
| vonmises(mu, kappa) | числа с распределением Майсеса (I- модифицированная функция Бесселя) |
| wald(mean, scale) | числа с распределением Вальда |
| weibull(a) | числа с распределением Вайбулла |
| zipf(a) | числа с распределением Зипфа (зетта функция Римана) |
ИГУМО и ИТ, Институт гуманитарного образования и информационных технологий
г. Москва
Факультет Фотографии
Факультет фотографии ИГУМО — единственный факультет в Москве, на котором готовят профессиональных фотографов по программе бакалавриата.
На факультете регулярно проходят мастер-классы знаменитых фотографов. Для студентов организуются выездные занятия и экскурсии по крупнейшим выставочным площадкам Москвы.
В рамках прохождения практики студенты факультета фотографии работают на крупных проектах. В 2016–2017 учебном году студенты проходили практику на 137-й Ассамблее Межпарламентского союза (Санкт-Петербург), в посольстве Индии, в посольстве Чешской Республики, на Всероссийском форуме «Наставник», на Втором Форуме социальных инноваций регионов, а также на конкурсе «Nikon: я в сердце изображения».
7.2. Линейная алгебра
NumPy предоставляет не только возможности для манипулирования многомерными массивами и их обработки, но еще и множество полезных математических функций, в том числе и функции линейной алгебры.
Произведение одномерных массивов представляет собой скалярное произведение векторов:
Произведение двумерных массивов по правилам линейной алгебры так же возможно:
При этом размеры матриц (массивов) должны быть либо равны, а сами матрицы квадратными, либо быть согласованными, т.е. если размеры матрицы равны , то размеры матрицы должны быть равны :
Так же по правилам умножения матриц, мы можем умножить матрицу на вектор (одномерный массив). При этом в таком умножении вектор столбец должен находиться справа, а вектор строка слева:
Квадратные матрицы можно возводить в степень т.е. умнажать сами на себя раз:
Довольно часто приходится вычислять ранг матриц:
Еще чаще приходится вычислять определитель матриц ,хотя результат вас может немного удивить:
В данном случае, из-за двоичной арифметики, результат не целое число и округлять до ближайшего целого прийдется вручную. Это связано с тем, что алгоритм вычисления определителя использует LU-разложение — это намного быстрее чем обычный алгоритм, но за скорость все же приходится немного заплатить ручным округлением (конечно, если таковое требуется):
Транспонирование матриц:
Вычисление обратных матриц:
Решение систем линейных уравнений:
Runtastic
Основные понятия и идеи нарративного подхода
Метафора нарратива, представляющая собой последовательность событий во времени, объединенных темой и сюжетом, является ключевой для понимания жизненных событий и переживаний людей в нарративном подходе. Нарративный практик ставит перед собой цель — создать условия для насыщенного описания предпочитаемой истории человека, обратившегося за консультацией.
По мнению нарративных терапевтов, «объективная реальность» является труднопостижимой. Любое знание, которое имеется у человека, по мнению нарративных терапевтов, есть знание с определенной позиции
Что важно, так это то, что необходимо учитывать социальный, культурный и исторический контекст, в котором оно порождается. В логике нарративного подхода принято считать, что жизнь каждого человека полиисторична
В ней разные истории состязаются за право быть в привилегированном положении, какая-то из них доминирует. Если доминирующая история является препятствием для развития, можно говорить о существовании проблемы
В логике нарративного подхода принято считать, что жизнь каждого человека полиисторична. В ней разные истории состязаются за право быть в привилегированном положении, какая-то из них доминирует. Если доминирующая история является препятствием для развития, можно говорить о существовании проблемы .
Также нарративные терапевты указывают на наличие опыта, не включенного в историю. Из него можно собрать истории, альтернативные доминирующей, и выяснить, какая из них является предпочитаемой. «Исключения» из такой проблемной истории в нарративном подходе называют «уникальными эпизодами»[неавторитетный источник?].
Помимо этого сторонники нарративного подхода полагают, что любое проявление опыта основывается на отличии этого опыта от его иного, от того, что можно назвать «отсутствующим, но подразумеваемым» в этом опыте. Так, человек говорит об отчаянии, потому что он может сравнить «отчаяние» с чем-то известным ему, что отчаянием не является. Например с «радостью» или «уверенностью в завтрашнем дне».
Так как не существует правильных историй, которые подходят всем, терапевт не может знать, что такое «правильное» развитие вообще и для данного человека в частности. Один из самых главных принципов гласит: терапевт не занимает экспертную позицию в жизни человека, сам клиент является экспертом.
Терапевт (или «практик», как многие из них предпочитают себя называть) не навязывает тому, кто обратился за помощью (слово «клиент» тоже не употребляется»), никаких методов, которые сам считает правильными. Задача терапевта состоит в том, чтобы человек выбрал из нескольких альтернативных направлений развития беседы тот, который больше нравится самому клиенту. За счет этого происходит укрепление контактов с теми ценностями и принципами, которые являются для него наиболее важными в предпочитаемых историях его жизни. Терапевт, выступая в качестве соавтора, является экспертом не по содержанию опыта человека, с которым ведется работа, а по задаванию вопросов.
Позиция терапевта является децентрированной и влиятельной. Это означает, что центральной фигурой всегда будет клиент, его ценности, знания, опыт и умения. За счет своих вопросов консультант создает пространство для выяснения различий. Он отчетливо осознает отношения властной позиции и противостоит злоупотреблению ею.
Занимая «неэкспертную» позицию, терапевт делает особый акцент на уважительное любопытство, что задает неиерархичность нарративного сообщества. Это является достаточно необычным подходом. В сообществе нарративных практиков вы не найдете «лестницы», по которой необходимо взбираться, чтобы достичь определенных успехов и твое мнение считалось бы достойным внимания
Также среди нарративных практиков принята этика заботы о коллегах, а не этика контроля; принято уделять большое внимание тому, чтобы никто из коллег не чувствовал себя игнорируемым. Нарративные практики говорят о том, что даже когда они работают с человеком индивидуально, это все равно является работа с сообществом, которому он принадлежит
Пакеты в SciPy
В SciPy есть набор пакетов для разных научных вычислений:
| Название | Описание |
|---|---|
| Алгоритмы кластерного анализа | |
| Физические и математические константы | |
| Быстрое преобразование Фурье | |
| Решения интегральных и обычных дифференциальных уравнений | |
| Интерполяция и сглаживание сплайнов | |
| Ввод и вывод | |
| Линейная алгебра | |
| N-размерная обработка изображений | |
| Метод ортогональных расстояний | |
| Оптимизация и численное решение уравнений | |
| Обработка сигналов | |
| Разреженные матрицы | |
| Разреженные и алгоритмы | |
| Специальные функции | |
| Статистические распределения и функции |
Подробное описание можно найти в официальной документации.
Эти пакеты нужно импортировать для использования библиотеки. Например:
Прежде чем рассматривать каждую функцию в подробностях, разберемся с теми из них, которые являются одинаковыми в NumPy и SciPy.
Создание массивов
В NumPy существует много способов создать массив. Один из наиболее простых — создать массив из обычных списков или кортежей Python, используя функцию numpy.array() (запомните: array — функция, создающая объект типа ndarray):
>>> import numpy as np >>> a = np.array() >>> a array() >>> type(a) <class 'numpy.ndarray'>
Функция array() трансформирует вложенные последовательности в многомерные массивы. Тип элементов массива зависит от типа элементов исходной последовательности (но можно и переопределить его в момент создания).
>>> b = np.array(, 4, 5, 6]])
>>> b
array(,
])
Можно также переопределить тип в момент создания:
>>> b = np.array(, 4, 5, 6]], dtype=np.complex)
>>> b
array(,
])
Функция array() не единственная функция для создания массивов. Обычно элементы массива вначале неизвестны, а массив, в котором они будут храниться, уже нужен. Поэтому имеется несколько функций для того, чтобы создавать массивы с каким-то исходным содержимым (по умолчанию тип создаваемого массива — float64).
Функция zeros() создает массив из нулей, а функция ones() — массив из единиц. Обе функции принимают кортеж с размерами, и аргумент dtype:
>>> np.zeros((3, 5))
array(,
,
])
>>> np.ones((2, 2, 2))
array(,
],
,
]])
Функция eye() создаёт единичную матрицу (двумерный массив)
>>> np.eye(5)
array(,
,
,
,
])
Функция empty() создает массив без его заполнения. Исходное содержимое случайно и зависит от состояния памяти на момент создания массива (то есть от того мусора, что в ней хранится):
>>> np.empty((3, 3))
array(,
,
])
>>> np.empty((3, 3))
array(,
,
])
Для создания последовательностей чисел, в NumPy имеется функция arange(), аналогичная встроенной в Python range(), только вместо списков она возвращает массивы, и принимает не только целые значения:
>>> np.arange(10, 30, 5) array() >>> np.arange(, 1, 0.1) array()
Вообще, при использовании arange() с аргументами типа float, сложно быть уверенным в том, сколько элементов будет получено (из-за ограничения точности чисел с плавающей запятой). Поэтому, в таких случаях обычно лучше использовать функцию linspace(), которая вместо шага в качестве одного из аргументов принимает число, равное количеству нужных элементов:
>>> np.linspace(, 2, 9) # 9 чисел от 0 до 2 включительно array()
fromfunction(): применяет функцию ко всем комбинациям индексов
Copies and Views¶
When operating and manipulating arrays, their data is sometimes copied
into a new array and sometimes not. This is often a source of confusion
for beginners. There are three cases:
No Copy at All
Simple assignments make no copy of objects or their data.
>>> a = np.array(, ... 4, 5, 6, 7], ... 8, 9, 10, 11]]) >>> b = a # no new object is created >>> b is a # a and b are two names for the same ndarray object True
Python passes mutable objects as references, so function calls make no
copy.
>>> def f(x): ... print(id(x)) ... >>> id(a) # id is a unique identifier of an object 148293216 # may vary >>> f(a) 148293216 # may vary
View or Shallow Copy
Different array objects can share the same data. The method
creates a new array object that looks at the same data.
>>> c = a.view()
>>> c is a
False
>>> c.base is a # c is a view of the data owned by a
True
>>> c.flags.owndata
False
>>>
>>> c = c.reshape((2, 6)) # a's shape doesn't change
>>> a.shape
(3, 4)
>>> c, 4 = 1234 # a's data changes
>>> a
array(,
,
])
Slicing an array returns a view of it:
>>> s = a , 13 # spaces added for clarity; could also be written "s = a"
>>> s = 10 # s is a view of s. Note the difference between s = 10 and s = 10
>>> a
array(,
,
])
Deep Copy
The method makes a complete copy of the array and its data.
>>> d = a.copy() # a new array object with new data is created
>>> d is a
False
>>> d.base is a # d doesn't share anything with a
False
>>> d, = 9999
>>> a
array(,
,
])
Sometimes should be called after slicing if the original array is not required anymore.
For example, suppose is a huge intermediate result and the final result only contains
a small fraction of , a deep copy should be made when constructing with slicing:
>>> a = np.arange(int(1e8)) >>> b = a[:100.copy() >>> del a # the memory of ``a`` can be released.
If is used instead, is referenced by and will persist in memory
even if is executed.
Документация и учебники
- https://docs.scipy.org/doc/numpy/user/index.html — Numpy (+tutorial)
- — Numpy документация
- http://www.labri.fr/perso/nrougier/teaching/numpy/numpy.html — Numpy tutorial by Nicolas P. Rougier
- http://www.labri.fr/perso/nrougier/teaching/numpy.100/index.html — 100 упражнений по numpy
- Numpy_Python_Cheat_Sheet.pdf: шпаргалка на 1 лист А4
matrix-multiply-a.svg:
task_description.png:
| Attachment | |||||
|---|---|---|---|---|---|
| axes.png | manage | 21.8 K | 26 Mar 2017 — 12:03 | TatyanaDerbysheva | |
| Numpy_Python_Cheat_Sheet.pdf | manage | 176.4 K | 26 Mar 2017 — 14:57 | TatyanaDerbysheva | шпаргалка на 1 лист А4 |
| s1.png | manage | 3.0 K | 26 Mar 2017 — 19:47 | TatyanaDerbysheva | |
| s2.png | manage | 6.1 K | 26 Mar 2017 — 19:47 | TatyanaDerbysheva | |
| s3.png | manage | 3.0 K | 26 Mar 2017 — 19:47 | TatyanaDerbysheva | |
| s4.png | manage | 6.1 K | 26 Mar 2017 — 19:48 | TatyanaDerbysheva | |
| s5.png | manage | 6.1 K | 26 Mar 2017 — 19:48 | TatyanaDerbysheva | |
| s6.png | manage | 3.0 K | 26 Mar 2017 — 19:48 | TatyanaDerbysheva | |
| cumsum.png | manage | 41.0 K | 31 Mar 2017 — 19:59 | TatyanaDerbysheva | |
| matrix-multiply-a.svg | manage | 27.6 K | 31 Mar 2017 — 20:31 | TatyanaDerbysheva | |
| task_description.png | manage | 9.3 K | 31 Mar 2017 — 22:11 | TatyanaDerbysheva |
(с) Материалы раздела «Язык Си» публикуются под лиценцией GNU Free Documentation License.
Двумерные массивы
Выше везде элементами массива были числа. Но на самом деле элементами массива может быть что угодно, в том числе другие массивы. Пример:
a = b = c = z =
Что здесь происходит? Создаются три обычных массива , и , а потом создается массив , элементами которого являются как раз массивы , и .
Что теперь получается? Например, — это элемент №1 массива , т.е. . Но — это тоже массив, поэтому я могу написать — это то же самое, что , т.е. (не забывайте, что нумерация элементов массива идет с нуля). Аналогично, и т.д.
То же самое можно было записать проще:
z = , , ]
Получилось то, что называется двумерным массивом. Его можно себе еще представить в виде любой из этих двух табличек:
Первую табличку надо читать так: если у вас написано , то надо взять строку № и столбец №. Например, — это элемент на 1 строке и 2 столбце, т.е. -3. Вторую табличку надо читать так: если у вас написано , то надо взять столбец № и строку №. Например, — это элемент на 2 столбце и 1 строке, т.е. -3. Т.е. в первой табличке строка — это первый индекс массива, а столбец — второй индекс, а во второй табличке наоборот. (Обычно принято как раз обозначать первый индекс и — второй.)
Когда вы думаете про таблички, важно то, что питон на самом деле не знает ничего про строки и столбцы. Для питона есть только первый индекс и второй индекс, а уж строка это или столбец — вы решаете сами, питону все равно
Т.е. и — это разные вещи, и питон их понимает по-разному, а будет 1 номером строки или столбца — это ваше дело, питон ничего не знает про строки и столбцы. Вы можете как хотите это решить, т.е. можете пользоваться первой картинкой, а можете и второй — но главное не запутайтесь и в каждой конкретной программе делайте всегда всё согласованно. А можете и вообще не думать про строки и столбцы, а просто думайте про первый и второй индекс.
Обратите, кстати, внимание на то, что в нашем примере (массив, являющийся вторым элементом массива ) короче остальных массивов (и поэтому на картинках отсутствует элемент в правом нижнем углу). Это общее правило питона: питон не требует, чтобы внутренние массивы были одинаковой длины
Вы вполне можете внутренние массивы делать разной длины, например:
x = , , , [], ]
здесь нулевой массив имеет длину 4, первый длину 2, второй длину 3, третий длину 0 (т.е. не содержит ни одного элемента), а четвертый длину 1. Такое бывает надо, но не так часто, в простых задачах у вас будут все подмассивы одной длины.
(На самом деле даже элементы одного массива не обязаны быть одного типа. Можно даже делать так: , здесь нулевой элемент массива — сам является массивом, а еще два элемента — просто числа. Но это совсем редко бывает надо.)